Оглавление:
Интегрирование иррациональных функций
Определение 1. Функция вида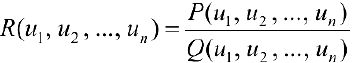 
где 
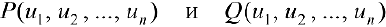многочлены от переменных 
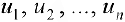, ми называются рациональными.
Задача №31
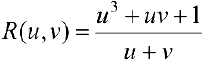— рациональпая функция переменных 
, при этом:
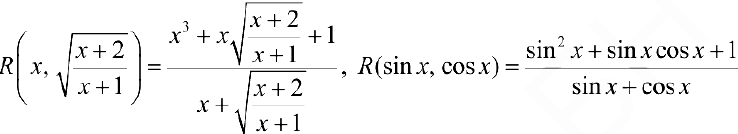
п.1. Интегралы вида:
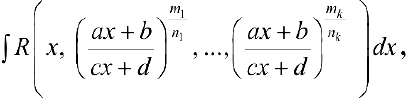, где 
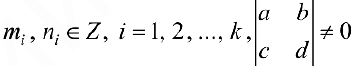и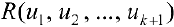 
— рациональная функция.
Пусть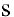 
— общий знаменатель дробей 
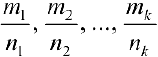. Тогда подстановка 
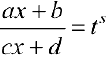делает подинтегральную функцию рациональной.
Задача №32
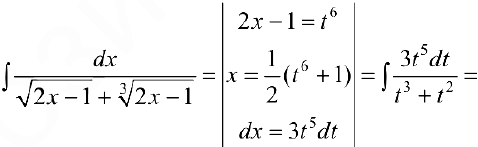
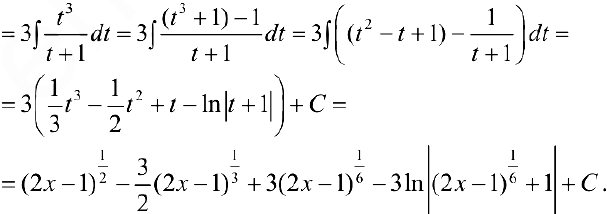
Задача №33
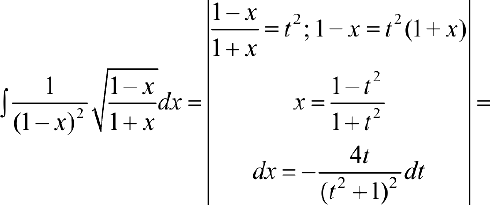
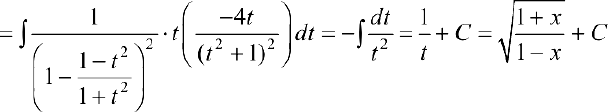
п.2. Интегралы вида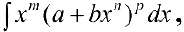 
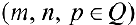— интегралы от дифференциального бинома.
Интегралы вида (1) выражаются через элементарные функции в следующих случаях:
а)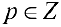 
— интегралы рассмотрены в п.1.
б)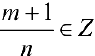 
, тогда подстановка 
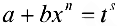, где s — знаменатель р приводит интегральную функцию к рациональной.
в)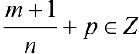 
, тогда подстановка 
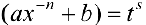, где s — знаменатель р приводит интегральную функцию к рациональной.
Во всех других случаях интегралы (1) выразить через элементарные функции нельзя (теорема Чебышева).
Задача №34
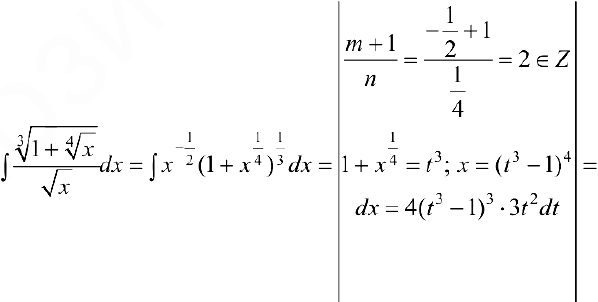
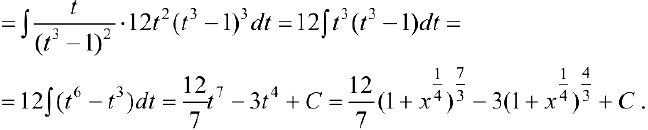
Задача №35
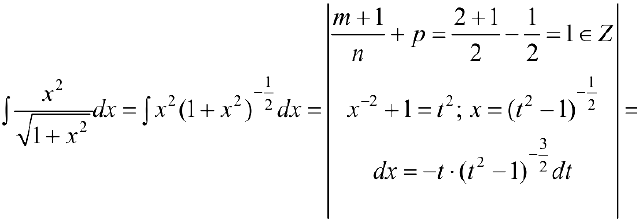
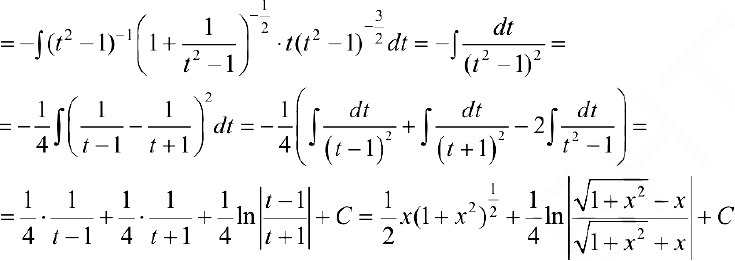
п.З. Интегралы вида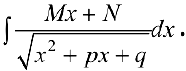 
Вычисление интегралов проводится аналогично интегралам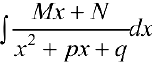 
выделением полного квадрата в трехчлене 
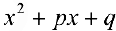(см. § 21, примеры 1, 2).
Задача №36
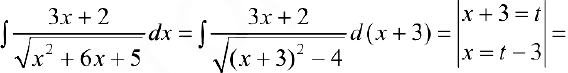
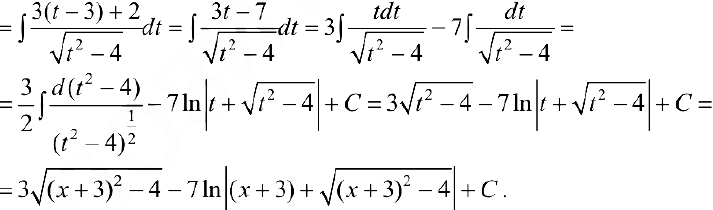
n 4. Интегралы вида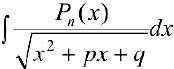 
, где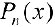 
— многочлен степени n.
Для вычисления интегралов используют равенство:
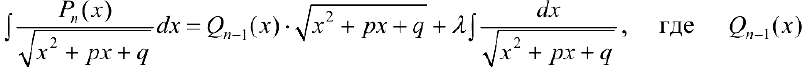
многочлен степени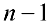 
. Коэффициенты многочлена 
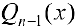, а также число 
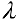находятся , если продифференцировать правую и левую часть равенства (2).
Задача №37
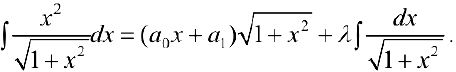После взятия производной:
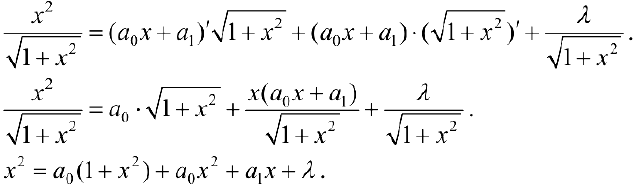
Приравниваем друг к другу коэффициенты при одинаковых степенях х в правой и левой частях.
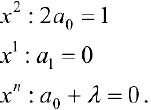
Решив систему (3), получим :
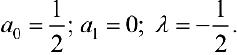. То есть
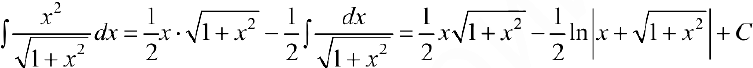(сравни с примером 5).
п.5. Интегралы вида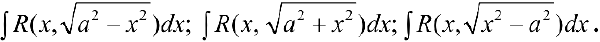 
В данных интегралах можно избавиться от иррациональности, если применить подходящую тригонометрическую или гиперболическую подстановку.
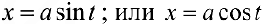— для первого интеграла,
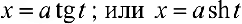— для второго,
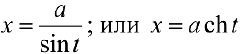— для третьего (см. § 23).
Задача №38
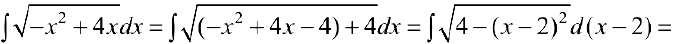
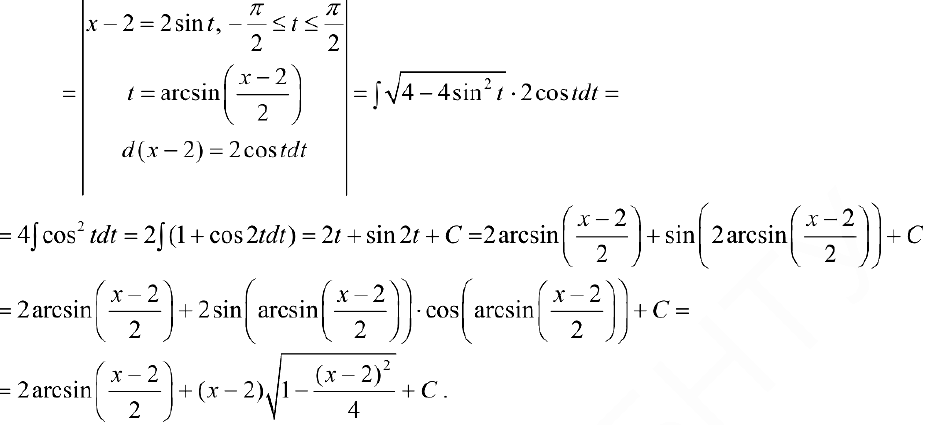
Задача №39
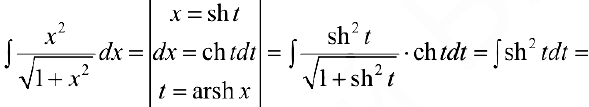
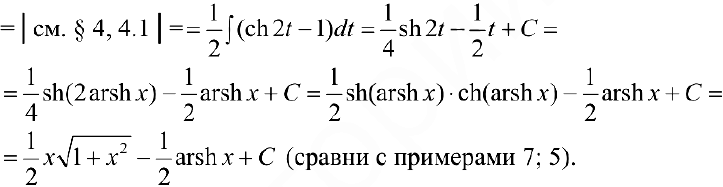
Эта теория и задачи с решением взяты со страницы готовых задач с решением по математическому анализу:
Решение задач по математическому анализу
Возможно эти темы вам будут полезны:
