Оглавление:
Задачи, приводящие к ситуации, когда дробь должна принимать целочисленные значения
Близкий подход связан с разрешением ситуации, когда некоторая дробь с целочисленными числителем и знаменателем должна быть целым числом. Это возможно лишь в случае, когда знаменатель принимает значения, равные целочисленным делителям числителя.
Пример №69.
На графике функции 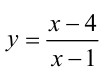 найти все точки, абсциссы и ординаты которых — целые числа.
найти все точки, абсциссы и ординаты которых — целые числа.
Решение:
Решим задачу без построения графика функции. Выделяя целую часть, преобразуем данную дробно-линейную функцию к виду:
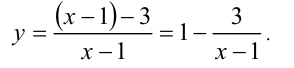
Поскольку у в последнем равенстве, по условию, принимает целочисленные значения и единица в правой части — также целое число, то, следовательно, дробь 3/(х — 1) также должна принимать целые значения. Это возможно тогда и только тогда, когда выражение x — 1 принимает значения всевозможных целых делителей числа 3, т.е. имеем 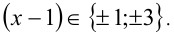 Отсюда находим четыре точки с целочисленными координатами:
Отсюда находим четыре точки с целочисленными координатами:
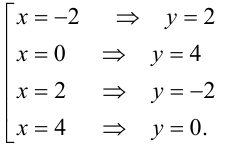
Ответ: 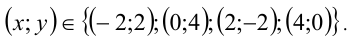
Пример №70.
Найти все пары целых чисел x и у , при которых является верным равенство 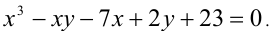
Решение:
Поскольку x = 2 , очевидно, не является решением уравнения, то приведём уравнение (оно линейно относительно у ) к эквивалентному виду:
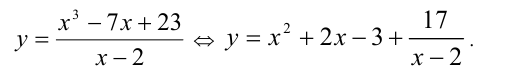
В силу целочисленности x,у, дробь 17/(х -2) должна быть целым числом, поэтому знаменатель x — 2 должен принимать значения целочисленных делителей числа 17, т.е. 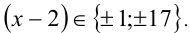 Рассмотрим каждый из этих случаев.
Рассмотрим каждый из этих случаев.
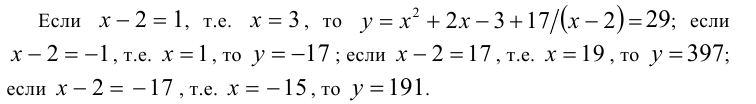
Ответ: 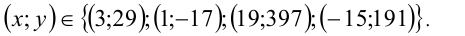
Эта лекция взята со страницы, где размещён подробный курс лекций по предмету математика:
Эти страницы возможно вам будут полезны:

