Оглавление:
Задачи, приводящие к дифференциальным уравнениям
Задача 1
Материальная точка массы 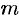 замедляет свое движение под действием силы сопротивления среды, пропорциональной квадрату скорости
замедляет свое движение под действием силы сопротивления среды, пропорциональной квадрату скорости 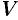 . Найти зависимость скорости от времени. Найти скорость точки через 3 с после начала замедления, если
. Найти зависимость скорости от времени. Найти скорость точки через 3 с после начала замедления, если 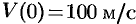 , a
, a 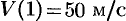 .
.
Решение:
Примем за независимую переменную время  , отсчитываемое от начала замедления движения материальной точки. Тогда скорость точки
, отсчитываемое от начала замедления движения материальной точки. Тогда скорость точки 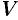 будет функцией
будет функцией  , т. е.
, т. е. 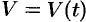 . Для нахождения
. Для нахождения 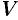 воспользуемся вторым законом Ньютона (основным законом механики):
воспользуемся вторым законом Ньютона (основным законом механики): 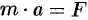 , где
, где 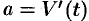 — есть ускорение движущегося тела,
— есть ускорение движущегося тела, 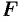 — результирующая сила, действующая на тело в процессе движения.
— результирующая сила, действующая на тело в процессе движения.
В данном случае 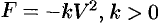 — коэффициент пропорциональности (знак минус указывает на то, что скорость тела уменьшается. Следовательно, функция
— коэффициент пропорциональности (знак минус указывает на то, что скорость тела уменьшается. Следовательно, функция 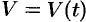 является решением дифференциального уравнения
является решением дифференциального уравнения 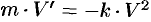 или
или 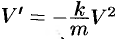 . Здесь
. Здесь 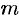 — масса тела.
— масса тела.
Как будет показано ниже (пример 48.5), 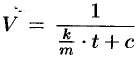 , где
, где 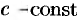 . Найдя зависимость скорости от времени, легко найти скорость точки через 3 с после начала замедления.
. Найдя зависимость скорости от времени, легко найти скорость точки через 3 с после начала замедления.
Найдем сначала параметры 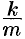 и
и 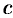 . Согласно условию задачи, имеем:
. Согласно условию задачи, имеем: 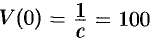 и
и 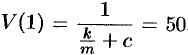 . Отсюда
. Отсюда 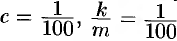 . Следовательно, скорость точки изменяется по закону
. Следовательно, скорость точки изменяется по закону  . Поэтому
. Поэтому 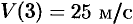 .
.
Задача 2
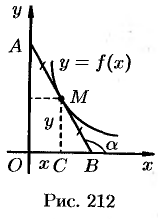
Найти кривую, проходящую через точку (4; 1), зная, что отреза любой касательной к ней, заключенный между осями координат, делится в точке касания пополам.
Решение:
Пусть 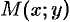 — произвольная точка кривой, уравнение которой
— произвольная точка кривой, уравнение которой  . Для определенности предположим, что кривая расположена в первой четверти (см. рис. 212).
. Для определенности предположим, что кривая расположена в первой четверти (см. рис. 212).
Для составления дифференциального уравнения воспользуемся геометрическим смыслом первой производной: 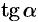 есть угловой коэффициент касательной; в точке
есть угловой коэффициент касательной; в точке 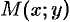 он равен
он равен 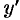 , т. е.
, т. е. 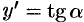 .
.
Из рисунка видно, что 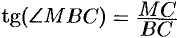 . Но
. Но
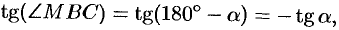
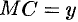 . По условию задачи
. По условию задачи 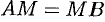 , следовательно,
, следовательно, 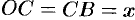 .
.
Таким образом, получаем 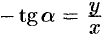 или
или 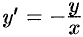 . Решением полученного дифференциального уравнения является функция
. Решением полученного дифференциального уравнения является функция 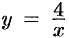 (гипербола). Решение будет приведено в п. 48.2 (пример 48.4).
(гипербола). Решение будет приведено в п. 48.2 (пример 48.4).
Другие задачи
Можно показать, что:
- закон изменения массы радия в зависимости от времени («радиоактивный распад») описывается дифференциальным уравнением
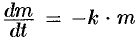 , где
, где 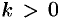 — коэффициент пропорциональности,
— коэффициент пропорциональности, 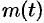 — масса радия в момент
— масса радия в момент  ;
; - «закон охлаждения тел», т. е. закон изменения температуры тела в зависимости от времени, описывается уравнением
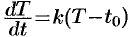 , где
, где 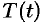 — температура тела в момент времени
— температура тела в момент времени 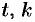 — коэффициент пропорциональности,
— коэффициент пропорциональности, 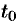 — температура воздуха (среды охлаждения);
— температура воздуха (среды охлаждения); - зависимость массы
 вещества, вступившего в химическую реакцию, от времени
вещества, вступившего в химическую реакцию, от времени  во многих случаях описывается уравнением
во многих случаях описывается уравнением 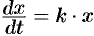 , где
, где 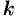 — коэффициент пропорциональности;
— коэффициент пропорциональности; - «закон размножения бактерий» (зависимость массы
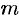 бактерий от времени
бактерий от времени  ) описывается уравнением
) описывается уравнением 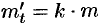 , где
, где 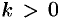 ;
; - закон изменения давления воздуха в зависимости от высоты над уровнем моря описывается уравнением
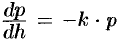 , где
, где 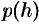 — атмосферное давление воздуха на высоте
— атмосферное давление воздуха на высоте 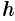 ,
, 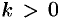 .
.
Уже приведенные примеры указывают на исключительно важную роль дифференциальных уравнений при решении самых разнообразных задач.
На этой странице размещён полный курс лекций с примерами решения по всем разделам высшей математики:
Другие темы по высшей математике возможно вам они будут полезны:
| Необходимые и достаточные условия экстремума |
| Наибольшее и наименьшее значения функции в замкнутой области |
| Уравнения с разделяющимися переменными |
| Однородные дифференциальные уравнения |

