Оглавление:
Задачи на совместную работу
Рассмотрим еще один тип задач — задачи на совместную работу (заполнение бассейна, перепечатка рукописи, рытье котлована и т.д.), которую выполняют несколько человек или механизмов, работающих с постоянной для каждого из них производительностью.
Примеры с решениями
Пример №204.
Грузчики А и В работали одинаковое число часов. Если бы грузчик А работал на 1ч меньше, а В — на 7 ч меньше, то А заработал бы 72 тыс. руб., а В — 64,8 тыс. руб. Если бы А работал на 7 ч меньше, а В — на 1ч меньше, то В заработал бы на 32,4 тыс. руб. больше, чем А. Сколько заработал каждый грузчик ?
Решение:
Пусть за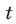 
часов работы грузчик А заработал 
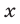тыс. руб., а В — 
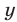тыс. руб. Используя условия задачи, составляем систему уравнений
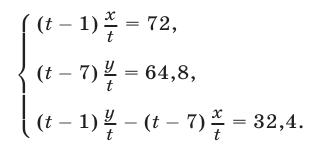
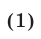
Из первых двух уравнений системы (1) находим
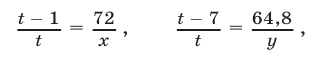
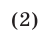
а из равенств (2) и третьего уравнения системы (1) получаем уравнение
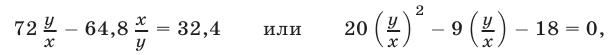
откуда
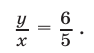
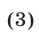
Разделив второе уравнение системы (1) на первое и учитывая равенство (3), получаем
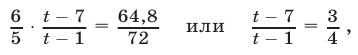
откуда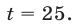 
Тогда из первого уравнения системы (1) находим, что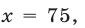 
а из (3) получаем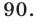 
Ответ. 75 тыс. руб. и 90 тыс. руб.
Пример №205.
Бак объемом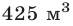 
был наполнен водой из двух кранов, причем первый кран был открыт на 5ч дольше второго. Если бы первый кран был открыт столько времени, сколько на самом деле был открыт второй, а второй кран был бы открыт столько времени, сколько был открыт первый, то из первого крана вытекло бы в 2 раза меньше воды, чем из второго. Если открыть два крана одновременно, то бак наполнится за 17 ч. Какое время был открыт второй кран?
Решение:
Пусть 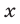— искомое время, 
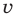и 
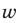— скорость поступления воды из первого и второго кранов соответственно ( 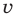и 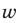измеряются в 
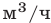). Тогда
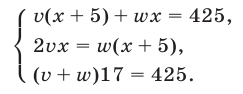
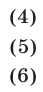
Из уравнений (4) и (5) находим
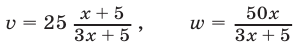
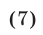
и подставляем выражения 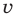и 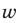, определяемые формулами (7), в уравнение (6).
Тогда получим квадратное уравнение
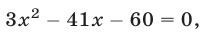
имеющее единственный положительный корень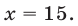 
Ответ. 15 ч.
Этот материал взят со страницы решения задач с примерами по всем темам предмета математика:
Возможно вам будут полезны эти страницы:
