Задачи на прямую

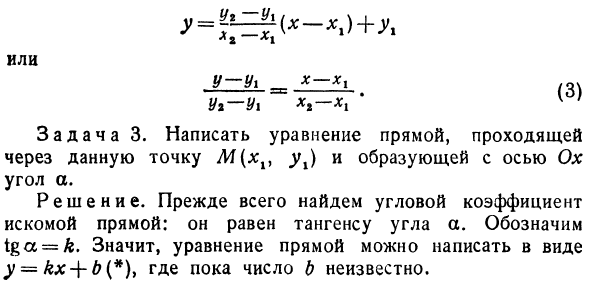
Задачи на прямую

• Прямая задача Задача 1. Найти угол y между двумя прямыми, заданный уравнением y = klx + bl, y = ktx + bt. Решения. На пересечении линий образуются четыре равных угла. Найти одного из них легко. Другое. Строки рисунка 16 обозначены (/) и (2) соответственно. Поскольку угол xAB является внешним по отношению к треугольнику ЛВС, он равен сумме двух внутренних углов треугольников, не смежных с ним. / HLV ASV + Z SVAU Откуда y = ^ CBA = ^ / xAB— -J / ACB = a1 — ал. Однако углы a и a не известны напрямую, а их касательные tgat = & lt tga2 = & 2 известны. Поэтому мы пишем tgY = tg (af — aj, или Рисунок 16.

Пример 1. Найти угол между линиями, заданный выражением y-2l; + 1, y = -Zlg. Здесь kl = -2y kt = –3; применяя уравнение (1), оно становится следующим. —3—2 — б, я TTT — 3J2) = —5 = Y = T- -3, при условии £ a = 2, 2 — (- 3) 1 3 tgY-i + (L3) 2: = ~ 1; Два ответа были получены. Если заданы две параллельные линии, углы a и a равны, поэтому их касательные также равны. тга ^ тга, т.е. кт = * кх.

Сначала был найден острый угол между указанными линиями, а затем был найден тупой угол. Людмила Фирмаль

Поэтому вывод таков: Если линии параллельны, угловые коэффициенты равны. Если линии вертикальные, угол между ними составляет 90 °. Но нет правильной касательной. Таким образом, уравнение (1) не должно давать ответа и возможно только в том случае, если знаменатель равен нулю (его нельзя разделить на ноль). 14- ^ = 0 или £ 1 ==: — * (2) Для.

Это условие перпендикулярности двух линий. Полезно запомнить это условие в следующей формулировке. Если две линии вертикальные, величина углового коэффициента меняется на противоположную, а знак меняется на противоположный. Пример 2. Нахождение угла между заданными линиями По уравнению y = Zl + 7 и y = — * — x + f. Если первый угловой коэффициент равен 3, второй Противоположный по размеру, но противоположный по знаку, Следовательно, рассматриваемая прямая линия является вертикальной.

• Задача 2. Даны две точки: Mx (xv y x) и M% (x1, yx)%. Где xxΦx% (то есть эти точки не находятся на прямой, параллельной оси Oy). Написать уравнение прямой через точки Mx и Mt. Решения. Поскольку интересующая линия не параллельна оси Oy, уравнение можно записать в виде y = kx + b (). Поэтому для решения задачи нам необходимо определить числа k и b.

() В уравнениях () и () все числа, кроме k и b, известны, поэтому эти уравнения можно рассматривать как систему уравнений для k и b. Решение системы показывает следующее: L-A = * (*, — *,). хх хх B = y. — Kx = y — yy до y1x. 1 1 1 хг — хх Подстановка выражения, найденного в выражении (*), приводит к следующему: От X2 до -Xl X1 — X1 1 Это линейное уравнение через две точки, которые не находятся на прямой, параллельной оси Oy.

Поскольку прямая проходит через точки Mx и M %%, координаты этих точек должны удовлетворять формуле (). yx = kxx + b} () yt = kxt + b. Людмила Фирмаль

Полученное уравнение находится в форме, удобной для запоминания, т.е.или U1 — U1 X1 — X1 v 7 Задача 3. Напишите линейное уравнение, которое проходит через заданную точку M (x19 yh) и образует угол a с осью Ox. Решения. Сначала найдите коэффициент угла искомой линии. Это равно тангенсу угла a. Указывает tga = &. Таким образом, линейное уравнение можно записать в виде y = kx + b (*) y. Здесь число b до сих пор неизвестно.

Поскольку прямая должна проходить через точку / H, координаты точки M удовлетворяют этому уравнению. ух = ххх + б. Если вы найдете здесь неизвестного b, вы получите b * = yx-kxx. Подставляя то, что находится в уравнении (), y = kx + yl-kxl или y — yx = k (x — xx). (4) Это уравнение прямой, проходящее через точку М в заданном направлении. Если вы измените направление уравнения (4) без изменения точки, вы получите уравнение для всех линий, которые проходят через указанную точку.

Уравнение y — yl = k (x — xx) называется уравнением карандаша прямой через точку M (xx, yx), где k — переменная, но xy и yy не изменяются. Пример 3. Напишите уравнение прямой, которое проходит через точку M (-2, 3) и образует угол 45 градусов с осью Ox. Поскольку tg45 ° = l, коэффициент угла равен 1. Xj = −2; y x == 3 «Уравнение линии записывается в виде Y-3 = 1 ( +2), или

Смотрите также:

Предмет высшая математика

Определение и геометрический смысл	Общее уравнение прямой. Неявная линейная функция
Основное свойство линейной функции	Система двух уравнений первой степени