Оглавление:


Задачи на применение определенного интеграла
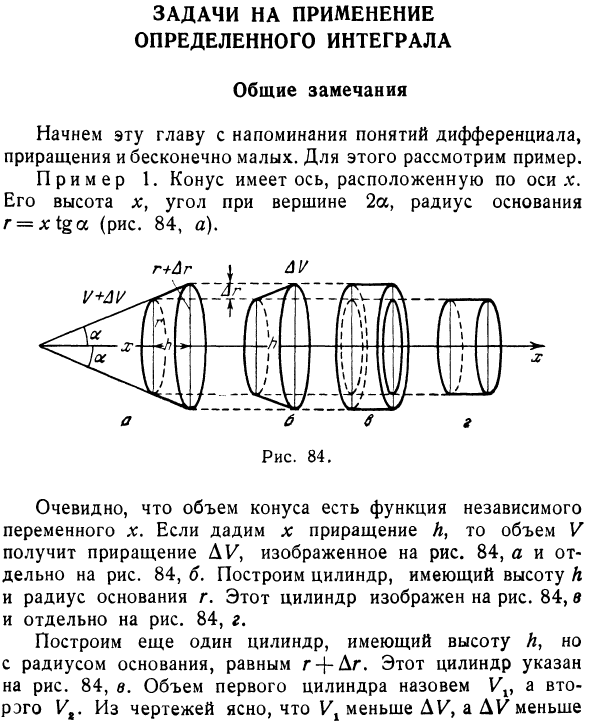
- Задачи для применения конкретных интеграций Общие замечания Эта глава начинается с понятий дифференцирования, приращения и бесконечно малого. Для этого рассмотрим пример. Пример 1. Конус имеет ось, расположенную вдоль оси *. Его высота x, угол вершины 2a, радиус основания r = xtga (фиг. 84, a). Рисунок 84. Очевидно, что объем конуса является функцией независимой переменной x. Если x задается с шагом h, том V получает приращение DV, как показано на рисунке 4. 84, а и фиг 84, б.
Давайте создадим цилиндр с высотой h и радиусом основания r. Этот цилиндр показан на рисунке. 84, с и цифра 84 г Создайте еще один цилиндр с высотой h, но с базовым радиусом, равным r + Dg. Этот цилиндр показан на рисунке. 84, эл. Объем первого цилиндра называется Vv, а объем второго цилиндра — Vt. Из чертежа ясно, что V1 меньше DC и меньше DC.
- Следовательно, приращение перепада давления отличается от объема Vx меньше, чем объем цилиндрической трубки (рис. 84, в). Объем цилиндрической трубки VTp с точностью до бесконечно малых более высоких порядков (см. П. 2 в части 5 главы IX) VT ^ 2nHrh. = = ,, r-r, = == — г, тт ^ 2πЛДДг применительно к обозначениям рассматриваемого примера. Однако Ar = / * tga (рис. 84, i), то есть Ktr ^ 2agL2 tga, что означает, что объем цилиндрической трубки является минимумом высокого порядка относительно h.
Следовательно, объем цилиндра Vx отличается от приращения AV на небольшую степень выше, чем h. Поэтому показано, что Vy представляет собой разницу в объеме конуса: dV = Vl-nr * h.
В этой главе всегда используются аргументы, похожие на сохраненные аргументы. Людмила Фирмаль
Смотрите также:
| Вычисление определенного интеграла при помощи первообразной функции | Площадь криволинейной трапеции |
| Свойства определенного интеграла | Объем тела вращения |

