Оглавление:
Задачи, использующие понятия наименьшего и наибольшего из двух или нескольких чисел
Иногда в условиях задач встречаются обозначения вида
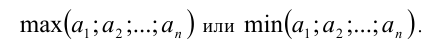
Под этими обозначениями, если не оговорено противное, обычно понимают наибольшее и, соответственно, наименьшее из 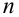 действительных чисел
действительных чисел 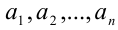 . В простейшей ситуации, когда количество чисел равно двум, для раскрытия этого понятия в задаче достаточно рассмотреть два случая, когда одно из чисел больше либо равно или меньше другого.
. В простейшей ситуации, когда количество чисел равно двум, для раскрытия этого понятия в задаче достаточно рассмотреть два случая, когда одно из чисел больше либо равно или меньше другого.
Пример №341.
Построить на плоскости 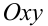 геометрическое место точек
геометрическое место точек 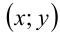 , координаты которых удовлетворяют уравнению
, координаты которых удовлетворяют уравнению
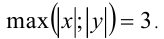
Решение:
Перейдём от уравнения к равносильной ему совокупности, раскрыв понятие наибольшего из двух чисел 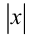 и
и 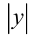 по определению:
по определению:
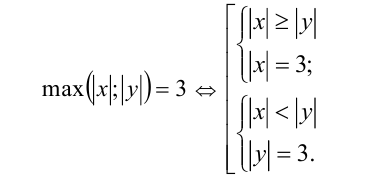
Далее строим геометрические образы решений первой и второй систем, это будут соответственно объединения отрезков, изображенных на рисунке:
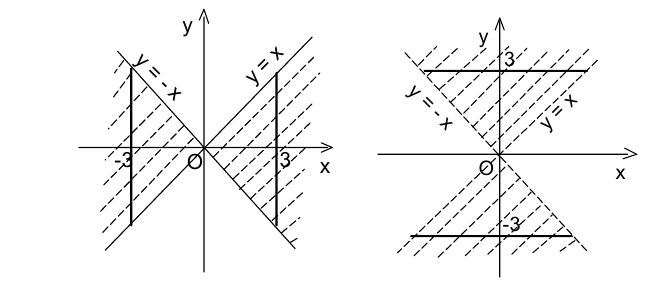
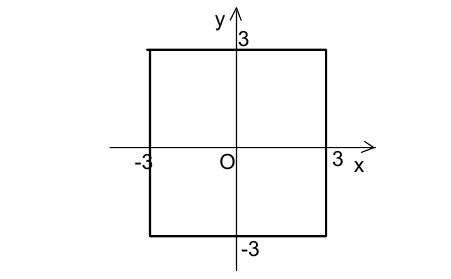
Объединяя все полученные отрезки, получаем искомое ГМТ в виде границы квадрата с центром в начале координат и сторонами длины 6, параллельными координатным осям. Задача решена.
В других ситуациях можно поступить иначе. Рассмотрим пример.
Пример №342.
Построить график функции 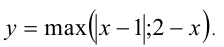
Решение:
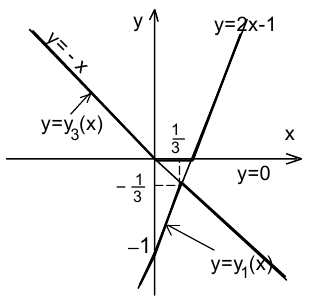
Построим в одной системе координат графики обеих функций 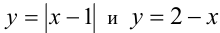 , найдём единственную точку их пересечения, её абсцисса равна
, найдём единственную точку их пересечения, её абсцисса равна 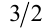 .
.
При 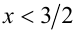 график функции
график функции 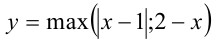 будет совпадать с графиком функции
будет совпадать с графиком функции 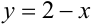 , а при
, а при 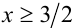 искомый график будет совпадать с графиком функции
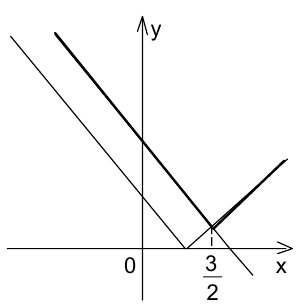
искомый график будет совпадать с графиком функции 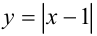 (т.е. на каждом из участков выбираем тот из графиков, который лежит выше). В результате получаем график функции
(т.е. на каждом из участков выбираем тот из графиков, который лежит выше). В результате получаем график функции 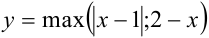 , который на рисунке обозначен полужирной линией.
, который на рисунке обозначен полужирной линией.
Если в задаче идет речь о наименьшем или наибольшем из двух действительных чисел, то иногда бывает удобно воспользоваться следующими тождествами.
Теорема. Для произвольных действительных чисел 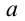 и
и 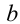 выполняются следующие тождества:
выполняются следующие тождества:
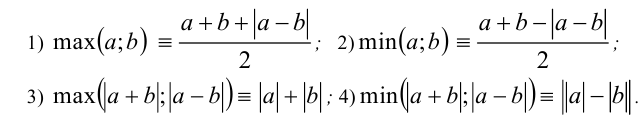
Доказательство. 1) Если 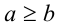 , то левая часть тождества, т.е.
, то левая часть тождества, т.е. 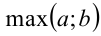 , равна
, равна 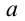 ; с другой стороны, правая часть тождества, т.е.
; с другой стороны, правая часть тождества, т.е. 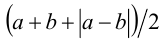 , после раскрытия модуля
, после раскрытия модуля 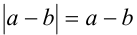 также оказывается равной
также оказывается равной 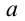 , что и доказывает данное тождество. Если же
, что и доказывает данное тождество. Если же 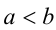 , то в левой части будет
, то в левой части будет 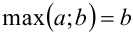 , и в правой части также
, и в правой части также
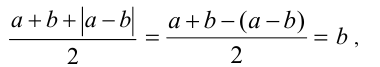
что подтверждает справедливость тождества и в этом случае.
2) Доказывается аналогично предыдущему случаю.
3) Если 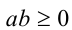 , то
, то 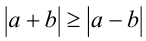 , и тождество принимает вид
, и тождество принимает вид 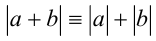 , что верно при всех
, что верно при всех 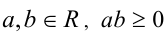 . Если же
. Если же 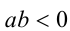 , то
, то 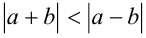 , и тождество принимает вид
, и тождество принимает вид 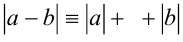 , что верно при всех
, что верно при всех 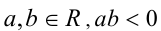 . Таким образом, справедливость тождества доказана при всех действительных
. Таким образом, справедливость тождества доказана при всех действительных 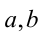 .
.
4) Доказывается аналогично предыдущему случаю.
Пример №343.
Решить уравнение
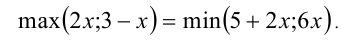
Решение:
Воспользуемся доказанными выше тождествами:
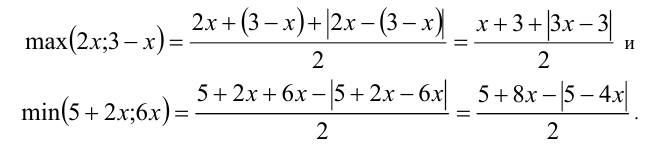
Тогда исходное уравнение равносильно уравнению
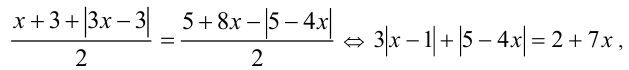
которое можно решить методом интервалов. Ответ: 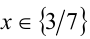 .
.
В ряде случаев при решении подобного рода задач удобно использовать свойства наибольшего и наименьшего из нескольких чисел. Например, для произвольных действительных чисел 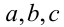 справедливы следующие свойства:
справедливы следующие свойства:
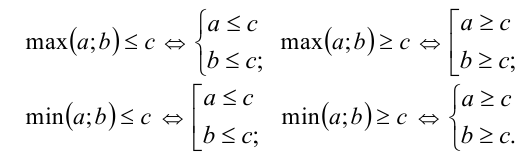
В самом деле, докажем первое из них. Начнём с необходимости. Пусть наибольшее из двух чисел 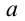 и
и 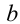 не превышает числа
не превышает числа 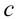 , тогда, очевидно, и каждое из чисел
, тогда, очевидно, и каждое из чисел 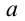 и
и 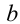 не будет превышать числа
не будет превышать числа 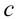 . Теперь докажем достаточность. Если каждое из чисел
. Теперь докажем достаточность. Если каждое из чисел 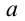 и
и 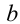 не превышает числа
не превышает числа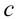 , то, значит, и наибольшее из них также не будет превышать это число. Таким образом, свойство доказано. Остальные свойства доказываются аналогичными логическими рассуждениями.
, то, значит, и наибольшее из них также не будет превышать это число. Таким образом, свойство доказано. Остальные свойства доказываются аналогичными логическими рассуждениями.
Пример №344.
Решить неравенство 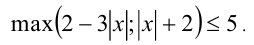
Решение:
Воспользуемся равносильным переходом:
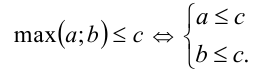
Применяя его, сразу сводим исходное неравенство к равносильной ему системе, решить которую уже не составляет труда:
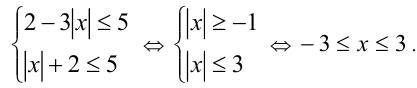
Пример №345.
Найти все значения 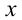 , удовлетворяющие неравенству
, удовлетворяющие неравенству
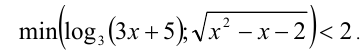
Решение:
Для решения задачи воспользуемся свойством
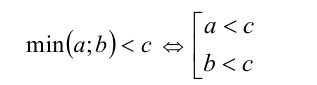
(убедитесь в том, что другие способы решения данной задачи существенно менее приемлемы). Естественно, применять указанное свойство можно только с учётом ОДЗ:
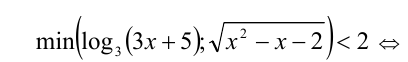
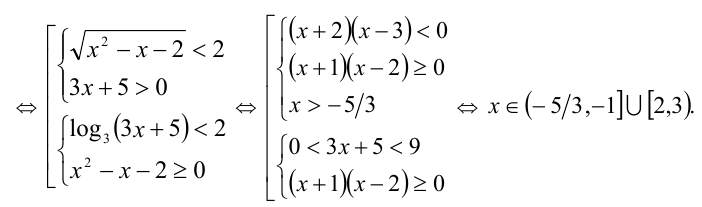
Пример №346.
Найти наименьшее значение выражения
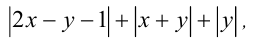
где 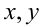 — произвольные действительные числа.
— произвольные действительные числа.
Решение:
Заметим, что при фиксированном 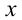 выражение
выражение
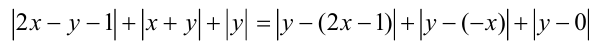
не меньше чем
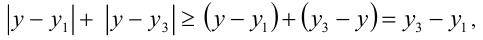
где 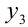 — наибольшее, a
— наибольшее, a 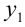 — наименьшее из трёх чисел
— наименьшее из трёх чисел 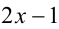 ,
, 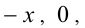 , при этом своё наименьшее значение
, при этом своё наименьшее значение 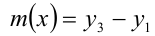 оно принимает при
оно принимает при 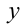 , равном среднему
, равном среднему 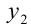 из тех же чисел. В свою очередь, наименьшее значение функции
из тех же чисел. В свою очередь, наименьшее значение функции 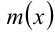 достигается при
достигается при 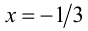 (см. рис.) и равно
(см. рис.) и равно 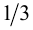 . Ответ:
. Ответ: 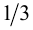 .
.
Пример №347.
Решить уравнение
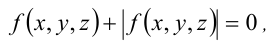
где 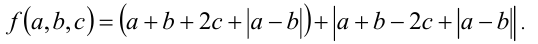
Решение:
Исходное неравенство, очевидно, равносильно неравенству
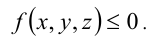
Обозначим для краткости 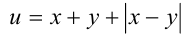 , тогда из определения
, тогда из определения 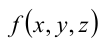 следует, что последнее неравенство равносильно
следует, что последнее неравенство равносильно
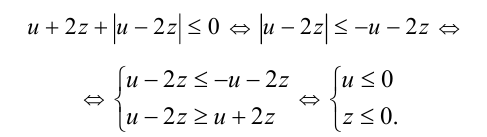
Аналогичными преобразованиями решаем неравенство 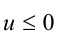 :
:
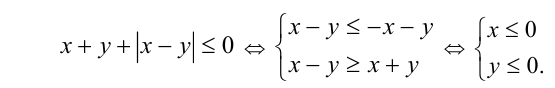
Так как 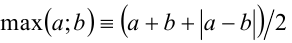 , то
, то
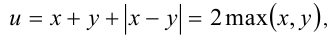
следовательно,
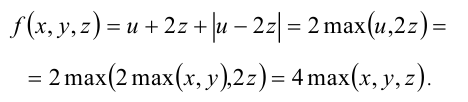
Отсюда
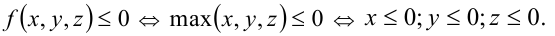
Ответ: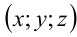 , где
, где 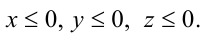
Эта лекция взята со страницы, где размещён подробный курс лекций по предмету математика:
Эти страницы возможно вам будут полезны:

