Задача В15. В 3 л воды при 40 °C бросили 50 г льда при -4 °C

Задача В15. В 3 л воды при 40 °C бросили 50 г льда при -4 °C. Какая установилась температура после того, как весь лед растаял? Удельная теплоемкость воды 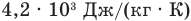, удельная теплоемкость льда 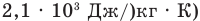, удельная теплота плавления льда .

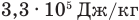Обозначим 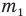массу воды, в которую бросили лед, — начальную температуру воды, 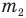— массу льда, t2 — начальную температуру льда, 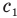— удельную теплоемкость воды, 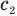— удельную теплоемкость льда, 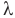— удельную теплоту плавления льда, 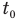— температуру плавления льда, t — установившуюся температуру, 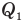— количество теплоты, которое отдает горячая вода, остывая от температуры 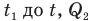— количество теплоты , полученное льдом при нагревании от 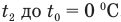, 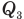— количество теплоты, полученное льдом при плавлении, 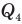— количество теплоты, полученное водой, образовавшейся из растаявшего льда при нагревании от 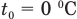до искомой температуры t.

Решение:

Следует знать, что 1 л воды имеет массу 1 кг, поэтому мы вместо объема 3 л записали массу воды 3 кг, ведь в формулах количеств теплоты везде стоит масса.

Для решения этой задачи воспользуемся законом сохранения тепловой энергии, ведь здесь не идет речь о КПД процесса, и значит, сумма всех отданных количеств теплоты одними телами равна сумме всех количеств теплоты, полученных другими. В нашей задаче отдает количество теплоты 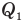только горячая вода, остывая от температуры 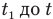, поэтому

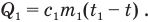
Получает эту теплоту лед. Поскольку он был при отрицательной температуре, то сначала он нагревается от 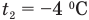до 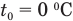(выше О °C лед нагреть нельзя, он при этой температуре тает). Поэтому количество теплоты, полученное льдом при нагревании,

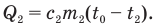
Поскольку тепло продолжает поступать от остывающей воды, лед тает. При этом он получает количество теплоты

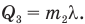
Далее, вода, образовавшаяся из растаявшего льда и потому имеющая такую же массу 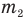, начнет нагреваться от 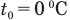до искомой температуры t и при этом получит количество теплоты

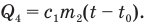
Теперь запишем закон сохранения тепловой энергии:

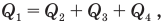
в который подставим вместо количеств теплоты правые части предыдущих равенств:

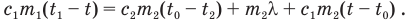
Полученное уравнение называется уравнением теплового баланса. Из него, раскрыв скобки там, где есть искомая температура t, найдем ее, поскольку остальные величины нам известны:

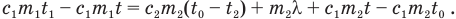
Последний член этого уравнения 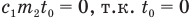. Из оставшегося выражения найдем t:

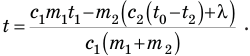
Мы решили задачу в общем виде. Произведем вычисления:

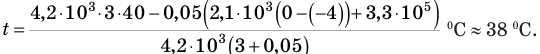
Ответ: .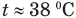

Эта задача взята со страницы подробного решения задач по физике, там расположена теория и подробное решения задач по всем темам физики:

Задачи по физике с решением

Возможно вам будут полезны эти задачи:

Задача В13. В аудитории объемом температура воздуха повысилась с 20 “С до 30 °C. Атмосферное давление Па, молярная масса воздуха 0,029 кг/моль, Какая масса воздуха вышла из комнаты?

Задача В14. При переходе определенной массы газа из одного состояния в другое его давление уменьшается, а температура увеличивается. Как при этом меняется его объем?

Задача В16. В герметически закрытом сосуде находятся 5 моль идеального одноатомного газа при 27 °C. Какое количество теплоты надо передать этому газу, чтобы его давление увеличилось в 3 раза?

Задача В17. Какое количество теплоты нужно передать 2 моль идеального одноатомного газа, чтобы изобарно увеличить его объем в 3 раза, если начальная температура 300 К?