Задача В11. Спутник переходит на более удаленную от Земли круговую орбиту. Как при этом изменяются линейная скорость спутника на орбите, период его обращения, кинетическая энергия, потенциальная энергия? Полная механическая энергия спутника остается постоянной.
Для каждой из этих физических величин выберите характер изменения: а) увеличилась б) уменьшилась в) не изменилась.
Решение:
Когда спутник переходит на более удаленную орбиту, ее радиус R увеличивается. Ускорение спутника на орбите, которое является там ускорением свободного падения и одновременно центростремительным ускорением спутника, связано с радиусом орбиты формулой
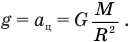
В свою очередь, центростремительное ускорение связано с линейной скоростью и радиусом орбиты формулой
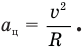
Приравняем правые части этих равенств:
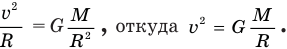
Поскольку гравитационная постоянная G и масса Земли М не меняются, значит, с увеличением радиуса орбиты R линейная скорость спутника уменьшается.
Линейная скорость связана с периодом спутника формулой
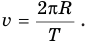
Подставив правую часть этого выражения в предыдущую формулу, получим:
Следовательно, при неизменных G и М с увеличением радиуса орбиты R период спутника увеличивается.
Кинетическая энергия спутника на орбите определяется формулой
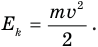
Значит, при уменьшении линейной скорости v и неизменной массе спутника m кинетическая энергия спутника уменьшается. А поскольку его полная механическая энергия, равная сумме кинетической энергии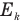 
и потенциальной энергии 
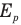не меняется, значит, с уменьшением кинетической энергии потенциальная энергия спутника увеличивается.
Ответ:
Эта задача взята со страницы подробного решения задач по физике, там расположена теория и подробное решения задач по всем темам физики:
Возможно вам будут полезны эти задачи:
