Задача СЗ. Колонна солдат длиной 20 м движется по шоссе со скоростью 3,6 км/ч. Командир, находящийся в хвосте колонны, посылает солдата с вопросом к сержанту, шагающему во главе колонны. Солдат бежит туда и обратно со скоростью, превышающей скорость колонны на 20%. Через сколько времени солдат доставит командиру ответ сержанта, если он слушал его в течение 0,5 мин?
Обозначим S длину колонны,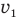 
— скорость колонны, 
— разность между скоростью солдата и скоростью колонны, t — время, в течение которого солдат слушал ответ сержанта, 
— время, в течение которого солдат доставит командиру ответ сержанта,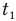 
— время, в течение которого солдат бежал к голове колонны, 
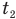— время, в течение которого солдат бежал обратно от головы колонны к командиру, 
— скорость солдата.
Решение:
Очевидно, что время 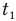, пока солдат бежал к голове колонны, не равно времени 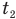, за которое он вернулся обратно, ведь, когда он бежал к голове, он обгонял колонну, а когда он бежал ей навстречу, она к нему приближалась, поэтому он пробежал ее длину быстрее.
Следовательно, искомое время 
можно представить как сумму трех времен: времени 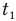пробега солдата к голове колонны, времени t, пока он разговаривал с сержантом, и времени 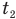его возвращения:
Судя по условию задачи, движение как колонны, так и солдата, было равномерным. Поэтому время 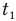, за которое солдат пробежал от хвоста колонны к ее голове, можно определить из формулы пути равномерного движения. Но при этом следует учесть, что скорость солдата относительно колонны в этом случае равна разности его скорости относительно дороги и скорости колонны 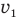относительно дороги. Поэтому время 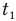равно:
где согласно условию 
, поэтому
Когда солдат побежал обратно, его скорость относительно приближавшейся к нему колонны стала равна сумме скорости колонны относительно дороги и его собственной скорости относительно нее, поэтому время, за которое он пробежал колонну обратно, равно:
Подставив правые части выражений (2) и (3) в равенство (1), мы решим задачу в общем виде:
Мы решили задачу в общем виде. Выразим все величины в единицах СИ: 
.
Подставим числа и вычислим:
Ответ: 
с.
Эта задача взята со страницы подробного решения задач по физике, там расположена теория и подробное решения задач по всем темам физики:
Возможно вам будут полезны эти задачи:
