Задача С9. Брусок массой М лежит на горизонтальном столе. Его пробивает пуля, летевшая параллельно поверхности стола со скоростью v. Пробив брусок, пуля вылетает в том же направлении с вдвое меньшей скоростью. При этом брусок передвигается по столу на расстояние S. Чему равен коэффициент трения бруска о поверхность стола?
Обозначим g ускорение свободного падения, 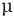 — коэффициент трения,
— коэффициент трения, 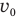 — начальную скорость бруска,
— начальную скорость бруска, 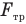 — силу трения между бруском и поверхностью стола, а — ускорение бруска,
— силу трения между бруском и поверхностью стола, а — ускорение бруска, 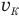 — конечную скорость бруска.
— конечную скорость бруска.
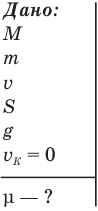
Решение:
Будем рассуждать так: пуля, пробив брусок, сообщила ему некоторую начальную скорость  , с которой он стал передвигаться равнозамедленно под действием силы трения.
, с которой он стал передвигаться равнозамедленно под действием силы трения.
По второму закону Ньютона сила трения между бруском и поверхностью стола равна произведению массы бруска и его ускорения:
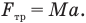
С другой стороны, сила трения равна произведению коэффициента трения и силы нормального давления бруска на поверхность стола, которая здесь равна силе тяжести, поэтому
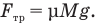
Приравняв правые части этих формул, получим:
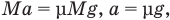
откуда
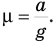
Таким образом, задача сводится к нахождению ускорения бруска (точнее, его замедления), когда он тормозил на пути S. В конце этого пути его скорость 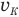 стала равна нулю, брусок остановился. Если бы мы знали его скорость
стала равна нулю, брусок остановился. Если бы мы знали его скорость 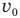 сразу после того, как пуля пробила брусок, мы могли найти нужное нам ускорение, записав так:
сразу после того, как пуля пробила брусок, мы могли найти нужное нам ускорение, записав так:
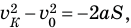
откуда при 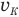 = 0
= 0
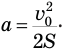
Теперь бы найти начальную скорость бруска сразу после пробивания его пулей. Для ее нахождения закон сохранения механической энергии применять нельзя, т.к. часть кинетической энергии пули прошла на пробивание бруска и превратилась в его внутреннюю энергию, да и пуля тоже могла нагреться. А вот закон сохранения импульса применить можно. Согласно этому закону импульс пули перед попаданием в брусок mv равен сумме импульса пули  после того, как она вылетела из него, и импульса бруска
после того, как она вылетела из него, и импульса бруска 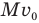 , полученного вследствие пробивания:
, полученного вследствие пробивания:
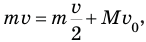
откуда
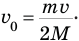
Подставим правую часть равенства (3) в формулу (2) вместо 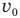 . Так мы выразим нужное нам для формулы (1) ускорение а через известные величины:
. Так мы выразим нужное нам для формулы (1) ускорение а через известные величины:
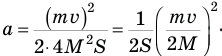
Нам осталось подставить правую часть этого равенства в формулу (1), и задача будет решена:
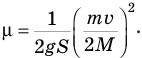
Задача решена.
Ответ: 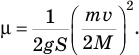 .
.
Эта задача взята со страницы подробного решения задач по физике, там расположена теория и подробное решения задач по всем темам физики:
Возможно вам будут полезны эти задачи:
