Задача С6. В цилиндре под двумя одинаковыми тонкими поршнями находится сжатый идеальный газ. Расстояния от дна цилиндра до нижнего поршня и от нижнего поршня до верхнего одинаковы и равны h. Давление воздуха под верхним поршнем вдвое больше атмосферного. Вся система находится в равновесии. На верхний поршень надавливают так, что он опускается на место нижнего, сжимая газ. Каким станет расстояние х от нижнего поршня до дна сосуда? Атмосферное давление постоянно.
Обозначим h расстояние от дна цилиндра до нижнего поршня и от нижнего поршня до верхнего перед надавливанием на верхний поршень, 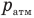 — атмосферное давление, х — расстояние от нижнего поршня до дна сосуда после надавливания,
— атмосферное давление, х — расстояние от нижнего поршня до дна сосуда после надавливания, 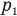 — давление воздуха под верхним поршнем до надавливания,
— давление воздуха под верхним поршнем до надавливания, 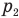 — давление воздуха под верхним поршнем после надавливания,
— давление воздуха под верхним поршнем после надавливания, 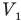 — объем воздуха под верхним поршнем до надавливания,
— объем воздуха под верхним поршнем до надавливания, 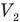 — объем воздуха под верхним поршнем после надавливания, S — площадь основания поршней и дна цилиндра,
— объем воздуха под верхним поршнем после надавливания, S — площадь основания поршней и дна цилиндра, 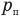 — давление поршня,
— давление поршня, 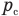 — давление силы, придавившей поршень,
— давление силы, придавившей поршень, 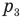 — давление воздуха под нижним поршнем до надавливания на верхний,
— давление воздуха под нижним поршнем до надавливания на верхний, 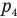 — давление воздуха под нижним поршнем после надавливания на верхний,
— давление воздуха под нижним поршнем после надавливания на верхний, 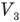 — объем воздуха под нижним поршнем после надавливания.
— объем воздуха под нижним поршнем после надавливания.
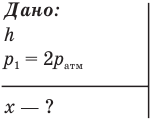
Решение:
Поскольку об изменении температуры нам ничего не сказано, мы имеем право считать процесс сжатия газа изотермическим. Значит, здесь можно применить закон Бойля — Мариотта, записав его применительно к газу сначала под верхним поршнем, потом под нижним (рис. 181, а и б).
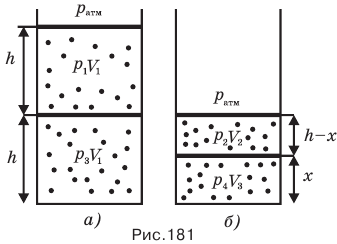
Закон Бойля — Мариотта применительно к газу под верхним поршнем будет выглядеть так:
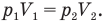
Давление газа под верхним поршнем 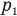 при равновесии равно сумме атмосферного давления
при равновесии равно сумме атмосферного давления 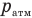 и давления поршня
и давления поршня 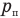 :
:

Но по условию задачи 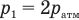 , поэтому
, поэтому
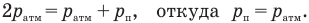
Объем воздуха под верхним поршнем вначале был равен:
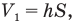
После опускания верхнего поршня на место нижнего газ под ними сжался и давление под верхним поршнем стало 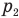 . Теперь оно равно сумме давлений атмосферы
. Теперь оно равно сумме давлений атмосферы 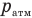 , поршня
, поршня 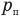 и некоторой силы, придавившей поршень,
и некоторой силы, придавившей поршень, 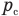 :
:
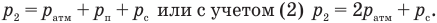
Новый объем воздуха под верхним поршнем станет равен:
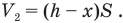
Подставим равенства 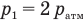 (3), (4) и (5) в формулу (1):
(3), (4) и (5) в формулу (1):

или после сокращения S

Теперь перейдем к газу под нижним поршнем. Запишем применительно к нему закон Бойля — Мариотта:
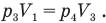
Давление газа под нижним поршнем 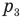 до опускания верхнего было равно сумме давления газа под верхним поршнем
до опускания верхнего было равно сумме давления газа под верхним поршнем 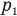 и давления самого нижнего поршня
и давления самого нижнего поршня 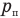 :
:
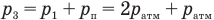
согласно условию задачи и равенству (2).
Поэтому 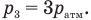
Давление газа 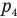 под нижним поршнем после его сжатия стало равно сумме давления газа под верхним поршнем
под нижним поршнем после его сжатия стало равно сумме давления газа под верхним поршнем 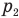 и давления самого нижнего поршня
и давления самого нижнего поршня 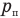 :
:
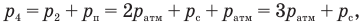
согласно (2) и (4).
Новый объем воздуха под нижним поршнем станет равен:

Подставим правые части равенств (8), (3), (9) и (10) в формулу (7):
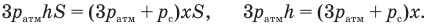
Теперь нам предстоит решить систему уравнений (6) и (11) относительно искомого расстояния х, исключив из них неизвестные давления. Давайте в этих уравнениях сначала раскроем скобки и сделаем приведение подобных членов, — может, мы их при этом немного упростим. Начнем с уравнения (6):
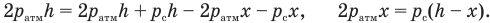
Теперь проделаем то же самое с уравнением (11):
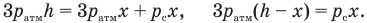
Если теперь разделить левые и правые части уравнений (12) и (13) друг на друга, то все неизвестные давления сократятся и мы сумеем найти расстояние х:
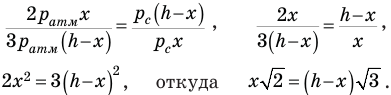
Отсюда 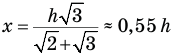 .
.
Ответ: 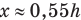 .
.
Эта задача взята со страницы подробного решения задач по физике, там расположена теория и подробное решения задач по всем темам физики:
Возможно вам будут полезны эти задачи:
