Задача С5. Маленький мячик бросили с земли под углом 60° к горизонту со скоростью 5 м/с в вертикальную стену, расположенную на расстоянии 1,5 м от места бросания. Под каким углом к горизонту отскочит мячик после абсолютно упругого удара о стену? Сопротивлением воздуха пренебречь.
Обозначим а угол между вектором начальной скорости мяча и горизонтом,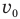 
— скорость бросания мяча, S — расстояние между местом бросания и стеной, g — ускорение свободного падения, 
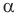— угол, под которым отскочит мячик после абсолютно упругого удара о стену, 
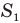— дальность полета мяча по горизонтали за время, пока он поднимался до высшей точки, 
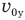— вертикальную составляющую скорости мяча в момент бросания, t — время его подъема до высшей точки, 
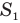— расстояние, которое пролетел мячик по горизонтали за время t, 
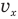— горизонтальную составляющую скорости мяча в момент бросания, 
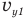— вертикальную составляющую скорости мяча в момент удара о стенку, и — скорость мяча в момент удара о стенку, 
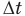— промежуток времени между моментом, когда мячик побывал в высшей точке, и моментом, когда он ударился о стену.
Решение:
Из теории мы знаем, что мячик, брошенный под углом к горизонту, движется вверх равнозамедленно, пока не достигнет высшей точки подъема, после чего начинает падать. И одновременно смещается по горизонтали, в результате чего его траекторией является парабола.
В нашем случае мячик, двигаясь по параболе, ударяется о стену. Зададимся вопросом: он на взлете ударился о стену или уже при спуске — ведь от этого зависит чертеж, который нам предстоит изобразить. Потому что если в условии задачи хоть что-то сказано об углах, то без подробного чертежа такую задачу не решить.
Чтобы уяснить, где траектория мяча упирается в стену, давайте вычислим, чему равняется дальность полета мяча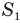 
по горизонтали за время, пока он поднимался до высшей точки. А потом сравним ее с расстоянием от точки бросания мяча до стены. И если эта дальность полета окажется больше расстояния до стены, то мячик ударился на взлете, а если меньше, — то уже при спуске.
Поскольку вертикальная составляющая скорости мяча в высшей точке равна нулю и поднимался он вверх равнозамедленно, то время его подъема до высшей точки найдем из формулы
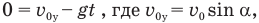
поэтому
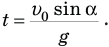
За это время мячик пролетел по горизонтали, двигаясь равномерно со скоростью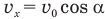 
расстояние 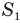Поэтому
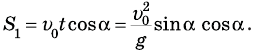
Вычислим это расстояние и сравним его с расстоянием S = 1,5 м до стены:
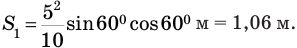
Это расстояние меньше расстояния 1,5 м до стены, значит, мячик ударился о стену уже после того, как побывал в высшей точке траектории. Теперь выполним чертеж (рис. 46).
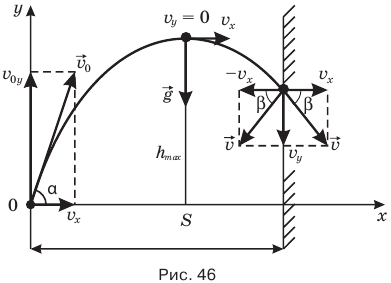
Поскольку удар был абсолютно упругим, угол, под которым мячик отскочит от стены, равен углу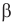 
, под которым он ударился, — это угол между вектором скорости мяча 
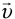в тот момент и перпендикуляром к стенке, который совпадает с горизонтальной проекцией скорости 
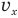. Из прямоугольного треугольника с гипотенузой, равной модулю вектора 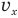, следует, что
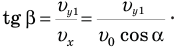
Таким образом, задача сводится к нахождению вертикальной составляющей скорости мяча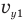 
. Если бы мы знали промежуток времени — обозначим его 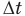t— между моментом, когда мячик побывал в высшей точке, и моментом, когда он ударился о стену, то проекцию скорости 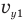мы нашли бы из формулы
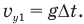
Значит, теперь надо найти этот промежуток времени 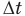. Его можно представить как разность времени полета мяча до удара о стену 
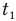, за которое он поднялся до высшей точки и успел опуститься перед ударом, и времени подъема до высшей точки t, которое мы уже определили по формуле (1):
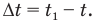
Время полета до стены равно времени равномерного перемещения мяча по горизонтали на расстояние S со скоростью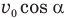 
, поэтому его можно найти так:
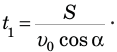
Теперь подставим правые части равенств (1) и (5) в выражение (4):
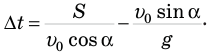
Нам осталось подставить правую часть выражения (6) в равенство (3), а то, что получится, — в выражение (2), — и задача в общем виде будет решена. Приступим. Подставляем (6) в(3):
Теперь подставляем (7) в (2):
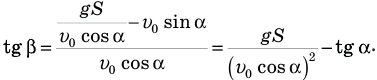
Задача в общем виде решена. Подставим числа и вычислим:
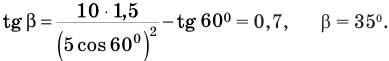
Ответ: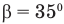 
Эта задача взята со страницы подробного решения задач по физике, там расположена теория и подробное решения задач по всем темам физики:
Возможно вам будут полезны эти задачи:
