Задача С5. Идеальный одноатомный газ, находящийся в теплоизолированном сосуде объемом Vпод давлениемр, заперт поршнем массой М (рис. 169). Справа поршень удерживают упоры 1 и 2, не давая газу расширяться. В поршень попадает пуля массой пг, летящая горизонтально со скоростью v, и застревает в нем. Считая, что всю механическую энергию поршень передаст газу, определить, во сколько раз повысится температура газа. Процесс в газе изобарный.
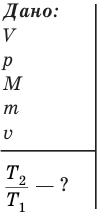
Обозначим 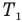 температуру газа до попадания пули в поршень,
температуру газа до попадания пули в поршень, 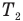 — температуру газа после попадания пули в поршень,
— температуру газа после попадания пули в поршень, 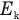 — кинетическую энергию поршня с застрявшей в нем пулей,
— кинетическую энергию поршня с застрявшей в нем пулей, 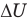 — увеличение внутренней энергии газа, А — работу изобарного сжатия газа, v — количество молей газа, R — молярную газовую постоянную,
— увеличение внутренней энергии газа, А — работу изобарного сжатия газа, v — количество молей газа, R — молярную газовую постоянную, 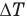 — изменение температуры газа после попадания пули в поршень. Остальные величины названы в условии задачи.
— изменение температуры газа после попадания пули в поршень. Остальные величины названы в условии задачи.
Решение:
Согласно условию задачи, вся кинетическая энергия поршня с застрявшей в нем пулей 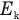 пойдет на увеличение внутренней энергии газа
пойдет на увеличение внутренней энергии газа 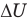 и на совершение отрицательной работы изобарного сжатия газа А:
и на совершение отрицательной работы изобарного сжатия газа А:
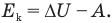
Воспользовавшись формулами кинетической энергии, внутренней энергии и работы изобарного изменения объема газа, запишем:
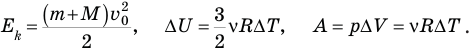
Здесь 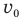
— скорость поршня с пулей сразу после попаданий в него пули. Подставив правые части этих выражений в предыдущую формулу, получим:
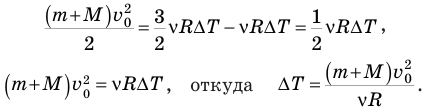
Искомое отношение 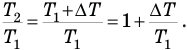
Начальную температуру газа 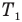 найдем из уравнения Менделеева — Клапейрона, записав его для первого состояния газа:
найдем из уравнения Менделеева — Клапейрона, записав его для первого состояния газа:
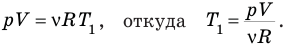
Подставим правые части равенств (1) и (3) в формулу (2):
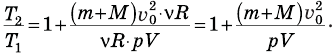
Нам осталось найти скорость поршня с пулей сразу после попадания в него пули. Ее мы найдем с помощью закона сохранения импульса, согласно которому импульс летящей пули mv равен импульсу поршня с застрявшей в нем пулей 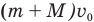 :
:
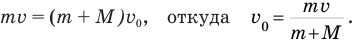
Подставим правую часть равенства (5) в выражение (4):
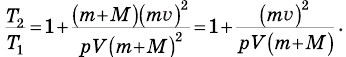
Задача решена.
Ответ: 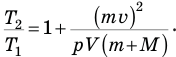
Эта задача взята со страницы подробного решения задач по физике, там расположена теория и подробное решения задач по всем темам физики:
Возможно вам будут полезны эти задачи:
