Задача С2. На краю горизонтальной доски, вращающейся вокруг вертикальной оси, проходящей через ее центр, укреплена нить с подвешенным к ней маленьким тяжелым шариком. Длина нити 20 см, частота вращения доски 1 об/с. При вращении доски нить отклоняется от вертикали на угол 30° (рис. 126). Найти длину доски. Ответ округлить до сотых долей метра.

Задача С2. На краю горизонтальной доски, вращающейся вокруг вертикальной оси, проходящей через ее центр, укреплена нить с подвешенным к ней маленьким тяжелым шариком. Длина нити 20 см, частота вращения доски 1 об/с. При вращении доски нить отклоняется от вертикали на угол 30° (рис. 126). Найти длину доски. Ответ округлить до сотых долей метра.

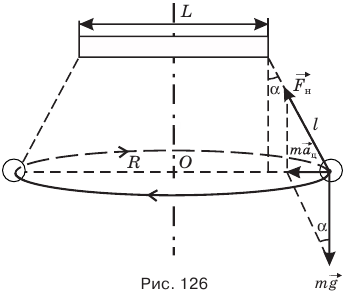
Обозначим I длину нити, v — частоту вращения стержня, 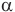— угол отклонения нити от вертикали, g — ускорение свободного падения, L — длину стержня, m — массу шарика, 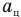— центростремительное ускорение шарика, 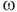— угловую скорость вращения стержня, R — радиус окружности, по которой движется шарик.

Решение:

На шарик действуют две силы: сила тяжести 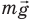и сила натяжения нити 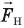. Их равнодействующая 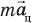направлена по радиусу к центру окружности О, по которой движется шарик. Ее модуль можно найти по формуле

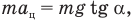
откуда

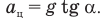
Ускорение шарика 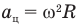, где угловая скорость шарика 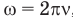, а радиус окружности .

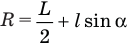С учетом этого ,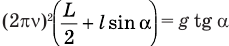

откуда

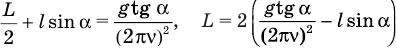
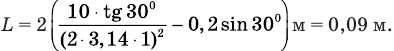
Ответ: L = 0,09 m.

Эта задача взята со страницы подробного решения задач по физике, там расположена теория и подробное решения задач по всем темам физики:

Задачи по физике с решением

Возможно вам будут полезны эти задачи:

Задача В11. Спутник переходит на более удаленную от Земли круговую орбиту. Как при этом изменяются линейная скорость спутника на орбите, период его обращения, кинетическая энергия, потенциальная энергия? Полная механическая энергия спутника остается постоянной.

Задача C1. К концам однородного стержня длиной Z = 1,8 м приложены силы (рис. 125). Найти силу натяжения стержня на расстоянии четверти длины от его левого конца.

Задача С3. Лыжник массой 80 кг спустился с горы высотой 30 м и после спуска проехал еще по горизонтальной поверхности до остановки 150 м (рис. 128). Найти силу сопротивления на горизонтальном участке, если на горе она была равна нулю.

Задача C4. Гиря, положенная сверху на вертикальную пружину, сжимает ее на 1 мм. Если эту гирю бросить на пружину со скоростью 0,2 м/с с высоты 10 см, то какова теперь будет деформация пружины?