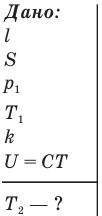
Задача С17. Посередине теплоизолированного и закрытого цилиндрического сосуда длиной l с площадью основания S располагается поршень, толщиной которого можно пренебречь. Справа от поршня в сосуде находится газ под давлением 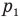 и при температуре
и при температуре 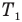 , а слева вакуум. Поршень соединен с левым основанием цилиндра сжатой упругой пружиной жесткостью k. Длина пружины в недеформированном состоянии равна длине цилиндра. Поршень удерживается в неподвижном состоянии внешним воздействием. Какая установится температура газа
, а слева вакуум. Поршень соединен с левым основанием цилиндра сжатой упругой пружиной жесткостью k. Длина пружины в недеформированном состоянии равна длине цилиндра. Поршень удерживается в неподвижном состоянии внешним воздействием. Какая установится температура газа 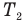 , если поршень отпустить? Известно, что внутренняя энергия этого газа пропорциональна его температуре: U = СТ, где С — известный коэффициент пропорциональности. Трением и теплоемкостями цилиндра с поршнем можно пренебречь.
, если поршень отпустить? Известно, что внутренняя энергия этого газа пропорциональна его температуре: U = СТ, где С — известный коэффициент пропорциональности. Трением и теплоемкостями цилиндра с поршнем можно пренебречь.
Обозначим 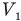 первоначальный объем газа, х — новую деформацию пружины,
первоначальный объем газа, х — новую деформацию пружины, 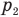 — новое давление газа на поршень,
— новое давление газа на поршень, 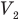 — новый объем газа.
— новый объем газа.
Решение:
Обратимся к рисунку (рис. 183) и подумаем. Газ давит на поршень справа, а пружина — слева. И при этом кто-то поршень еще и держит, а потом отпускает. Пружина, естественно, распрямляется, но не до конца.
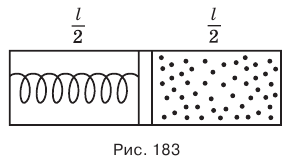
Потому что ее длина в недеформированном состоянии равна длине цилиндра, но там справа газ. Он и не даст ей распрямиться до конца. Газ сожмется, и его объем уменьшится. Сначала он занимал половину объема цилиндра, значит, его объем был равен произведению половины длины цилиндра и площади его основания:
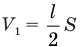
После частичного распрямления пружины поршень окажется в равновесии в новом положении. Это значит, что силы, давящие на него слева и справа, станут по модулю равны друг другу. Слева на поршень давит пружина, и сила ее давления равна силе упругости, возникающей в ней, но направлена противоположно. Тогда согласно закону Гука эта сила равна kx. А справа на поршень давит сжатый газ, сила давления которого равна произведению его нового давления 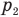 на площадь поршня, которая тоже равна S. Тогда мы можем записать условие равновесия поршня в новом положении так:
на площадь поршня, которая тоже равна S. Тогда мы можем записать условие равновесия поршня в новом положении так:
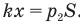
Нам надо найти новую температуру 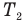 сжатого газа. Сосуд теплоизолирован, значит, процесс сжатия газа адиабатный. Следовательно, за счет адиабатного сжатия газа его температура повысится. Поскольку сосуд теплоизолирован, при перемещении поршня энергия этой системы тел сохраняется.
сжатого газа. Сосуд теплоизолирован, значит, процесс сжатия газа адиабатный. Следовательно, за счет адиабатного сжатия газа его температура повысится. Поскольку сосуд теплоизолирован, при перемещении поршня энергия этой системы тел сохраняется.
Когда поршень находился посередине цилиндра, его пружина была сжата и, значит, обладала потенциальной энергией. При этом ее деформация была равна разности между недеформированной длиной пружины, равной длине цилиндра l, и длиной наполовину сжатой пружины, которая равна 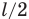 . Следовательно, деформация пружины в первом положении поршня тоже была
. Следовательно, деформация пружины в первом положении поршня тоже была 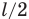 . Тогда потенциальная энергия пружины была равна
. Тогда потенциальная энергия пружины была равна 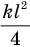 . Кроме того, газ обладал внутренней энергией
. Кроме того, газ обладал внутренней энергией 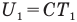 . Значит, полная энергия этой системы тел была равна
. Значит, полная энергия этой системы тел была равна
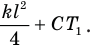
Когда пружину отпустили, она распрямилась, но не до конца. Значит, у нее остался запас потенциальной энергии. Теперь деформация пружины равна х, и значит, ее потенциальная энергия стала 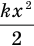 , а внутренняя энергия сжатого газа —
, а внутренняя энергия сжатого газа — 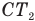 , и полная энергия системы равна
, и полная энергия системы равна
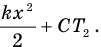
Тогда согласно закону сохранения энергии справедливо равенство
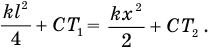
Как бы отыскать этот х? Он входит в условие равновесия (2), но там появляется неизвестное давление газа 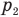 . Как бы его найти? Что мы еще не использовали?
. Как бы его найти? Что мы еще не использовали?
А мы не использовали газовые законы. У нас масса газа, запертого поршнем, не меняется. Значит, можно воспользоваться одним из газовых законов. Только каким? Когда поршень сжал газ, у того изменились и давление, и объем, и температура. Значит, мы можем применить объединенный газовый закон, записав его для первого и второго состояний газа, тем более, что в него войдут известные и искомая величины:
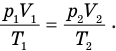
Новый объем газа 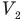 равен произведению расстояния от поршня до правого основания цилиндра и площади этого основания. А это расстояние равно деформации пружины. Значит,
равен произведению расстояния от поршня до правого основания цилиндра и площади этого основания. А это расстояние равно деформации пружины. Значит,
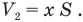
Теперь давайте подставим в формулу (4) значения 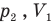 и
и 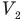 . Из формулы (2) имеем:
. Из формулы (2) имеем:
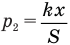
Подставляем правые части равенств (1), (5) и (6) в формулу (4). А давление 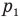 и температура
и температура 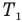 нам известны из условия. Посмотрим, что получится:
нам известны из условия. Посмотрим, что получится:
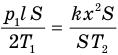 или после сокращения S
или после сокращения S 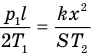
Итак, мы получили систему двух уравнений (3) и (7) с двумя неизвестными: ненужной деформацией х и нужной температурой 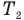 . Выразим из уравнения (7) произведение
. Выразим из уравнения (7) произведение 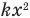 и то, что получится, подставим вместо него в уравнение (3):
и то, что получится, подставим вместо него в уравнение (3):
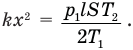
Теперь подставляем правую часть этого равенства в формулу (3) вместо 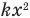 . Так мы получим одно уравнение с одной искомой температурой
. Так мы получим одно уравнение с одной искомой температурой 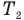 , которую оттуда и найдем. Вперед:
, которую оттуда и найдем. Вперед:
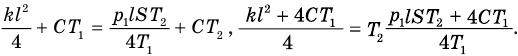
Отсюда
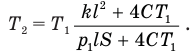
Ответ: 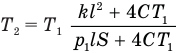 .
.
Эта задача взята со страницы подробного решения задач по физике, там расположена теория и подробное решения задач по всем темам физики:
Возможно вам будут полезны эти задачи:
