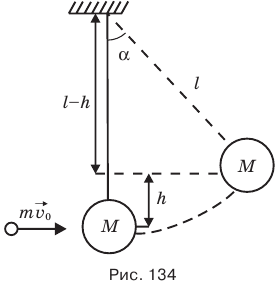
Задача С15. Шарик массой m, летящий горизонтально со скоростью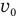 
, абсолютно упруго ударяется о неподвижный шар массой М, висящий на нити длиной l. Удар центральный. На какой угол отклонится шар массой М после удара (рис. 134)?
Обозначим h высоту, на которую поднимется шар массой М в результате удара,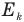 
— кинетическую энергию, которую приобретет шар массой М сразу после удара, 
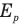— потенциальную энергию шара массой М на высоте h, g — ускорение свободного падения, 
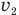— скорость, которую приобретет шар массой М сразу после удара, 
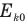— кинетическую энергию шарика массой m перед ударом, 
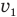— скорость шарика массой m после удара.
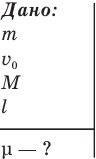
Решение:
В результате удара шар массой М поднимется на некоторую высоту h. Эту высоту несложно связать с углом отклонения шара, который мы ищем, и длиной нити, на которой висит шар.
Действительно, искомый угол а является углом при вершине прямоугольного треугольника с гипотенузой l и катетом l — h, прилежащим к этому углу, поэтому
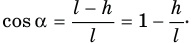
Теперь задача сводится к нахождению высоты h. Для ее определения удобно воспользоваться законом сохранения механической энергии. Его мы имеем право здесь применить, поскольку в системе упруго соударяющихся шаров действуют только консервативные силы тяжести и силы упругости. Кинетическая энергия 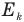, которую приобретет шар массой М сразу после удара, полностью превратится в его потенциальную энергию 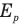на высоте h:
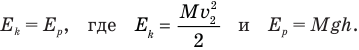
Поэтому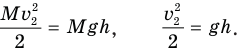 
.
Отсюда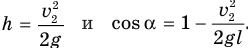 
Для определения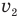 
снова можно воспользоваться законом сохранения механической энергии, примененным к обоим шарам, согласно которому кинетическая энергия 
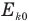шарика массой m перед ударом превращается в сумму кинетических энергий обоих шаров сразу после удара:
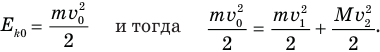
Очевидно, что решить это уравнение, т.е. однозначно найти скорость 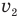шара массой М после удара мы не можем, так как это уравнение содержит две неизвестных величины 
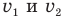. Поэтому нам необходимо записать еще одно уравнение, в которое вошли бы эти же величины, и тогда решить два уравнения с двумя неизвестными мы смогли бы. Такое уравнение нам дает закон сохранения импульса, согласно которому импульс 
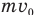шарика массой m до удара равен сумме импульса этого же шарика 
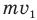и импульса 
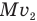шара массой М после удара. По закону сохранения импульса:
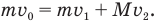
Теперь нам предстоит решить систему уравнений (2) и (3) с двумя неизвестными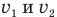 
. С первого взгляда кажется, что ничего сложного в этом решении нет, достаточно выразить ненужную нам неизвестную скорость 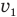, из уравнения (3) и подставить ее в уравнение (2). Тогда в нем останется только одна неизвестная скорость 
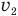, которую мы и найдем. Но на самом деле этот путь приведет к громоздкому решению, поэтому мы пойдем другим путем. Действия, которые мы проделаем, стоит запомнить, чтобы потом решать подобные задачи, не испытывая особых затруднений.
Перенесем слагаемые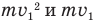 
в обоих уравнениях влево (сократив в уравнении (2) двойки в знаменателях):
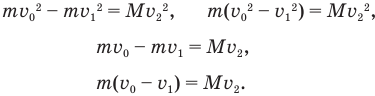
Теперь разделим левые и правые части уравнений (4) и (6) друг на друга:
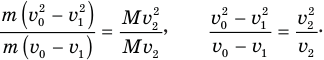
Поскольку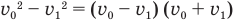 
, то, выполнив сокращения, получим:
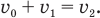
Умножим каждый член этого уравнения на m, а затем сложим полученное выражение с уравнением (5). При этом член, содержащий член, содержащий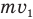 
, «уйдет» и мы легко найдем нужную нам скорость :
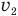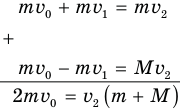
откуда
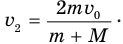
Нам осталось подставить полученное выражение в уравнение (1), и задача будет решена:
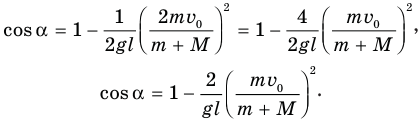
Ответ: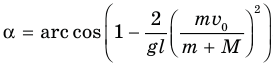 
Эта задача взята со страницы подробного решения задач по физике, там расположена теория и подробное решения задач по всем темам физики:
Возможно вам будут полезны эти задачи:
