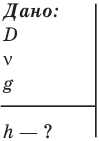
Задача С10. Внутри полого шара диаметром D находится маленький кубик. Шар вращается с частотой v вокруг оси 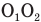 , проходящей через его центр. На какую высоту h поднимется кубик, перемещаясь по поверхности шара в процессе его вращения? Трением пренебречь.
, проходящей через его центр. На какую высоту h поднимется кубик, перемещаясь по поверхности шара в процессе его вращения? Трением пренебречь.
Обозначим g ускорение свободного падения, h — высоту, на которую поднимется кубик, m — массу кубика, 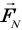 — силу реакции шара, R — радиус шара,
— силу реакции шара, R — радиус шара, 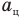 — центростремительное ускорение кубика, со — угловую скорость шара,
— центростремительное ускорение кубика, со — угловую скорость шара, 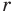 — радиус окружности, по которой движется кубик.
— радиус окружности, по которой движется кубик.
Решение:
На кубик, вращающийся вместе с шаром, действуют при отсутствии трения две силы: сила тяжести mg и сила реакции поверхности шара 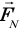 (рис. 132). По второму закону Ньютона в векторной записи
(рис. 132). По второму закону Ньютона в векторной записи
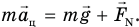
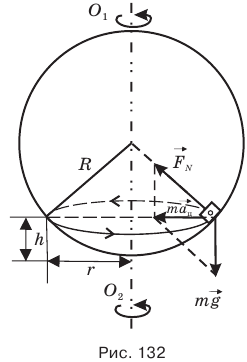
Нам надо определить высоту h, на которую поднимется кубик вследствие вращения шара. Если внимательно рассмотреть рис. 132, то можно увидеть два подобных прямоугольных треугольника. У одного из них, который поменьше, гипотенузой служит вектор 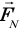 , а катетами — вектор
, а катетами — вектор 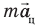 и штриховой отрезок, равный модулю силы тяжести mg. Во втором треугольнике гипотенузой является радиус шара
и штриховой отрезок, равный модулю силы тяжести mg. Во втором треугольнике гипотенузой является радиус шара 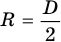 катетами — отрезок R — h и отрезок
катетами — отрезок R — h и отрезок 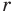 . Поскольку в подобных треугольниках стороны, лежащие против равных углов, пропорциональны, то
. Поскольку в подобных треугольниках стороны, лежащие против равных углов, пропорциональны, то

Выразим центростремительное ускорение 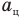 через частоту вращения шара v и радиус окружности
через частоту вращения шара v и радиус окружности 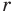 , по которой движется кубик:
, по которой движется кубик:
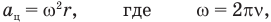
поэтому
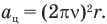
Подставим (2) в (1):
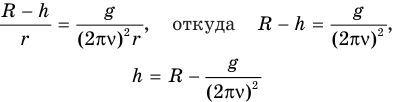
или, поскольку 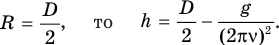
Проанализируем полученный результат. Высота h, на которую поднимется кубик, будет возрастать с увеличением частоты вращения v. Когда частота вращения станет бесконечно велика 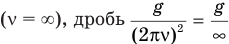 обратится в нуль, и тогда высота h будет равна радиусу
обратится в нуль, и тогда высота h будет равна радиусу 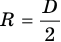 . Следовательно, кубик не сможет подняться на высоту, большую радиуса шара при любой частоте вращения.
. Следовательно, кубик не сможет подняться на высоту, большую радиуса шара при любой частоте вращения.
Ответ: 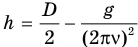
Эта задача взята со страницы подробного решения задач по физике, там расположена теория и подробное решения задач по всем темам физики:
Возможно вам будут полезны эти задачи:
