Замена переменной, интегрирование но частям в определенном интеграле

Замена переменной, интегрирование но частям в определенном интеграле

Теорема 1. Пусть функция 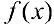— непрерывна на промежутке 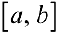и функция 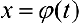— непрерывно-дифференцируема па промежутке 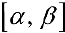,,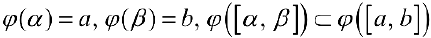 тогда

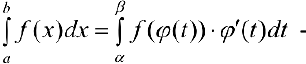
формула замены переменной.

Доказательство. Пусть 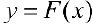— первообразная для 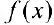на промежутке 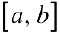, тогда (см. теорему 1 § 19) 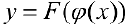— первообразная для 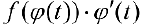на промежутке 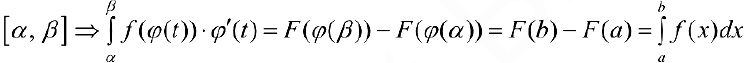что и требовалось доказать.

Задача №56

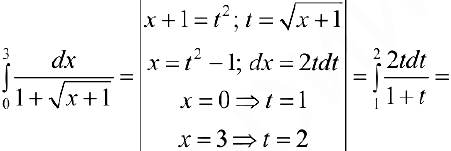
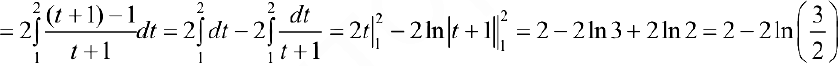
Теорема 2. Пусть функции 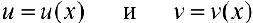непрерывно дифференцируемы на промежутке 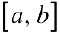, тогда

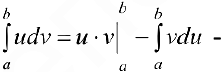
формула интегрирования по частям.

Доказательство. 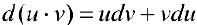(см. § 6). Поэтому ,

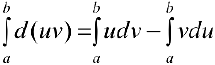но 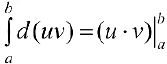(см. формулу(З) § 18) и теорема доказана.

Эта теория и задачи с решением взяты со страницы готовых задач с решением по математическому анализу:

Решение задач по математическому анализу

Возможно эти темы вам будут полезны:

Доказательство с решением по теме: свойства определенного интеграла

Задачи с решением по теме: формула Ньютона -Лейбница

Задачи с решением по теме: несобственные интегралы первою рода

Задачи с решением по теме: несобственные интегралы второго рода