Оглавление:

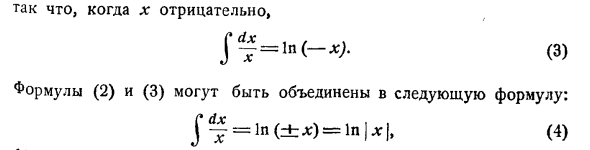

Задача практического интегрирования
- Практическое интеграционное задание. Результат первой части этой главы позволяет вам быстро написать несколько простых интегралов функций. так J xmdx = ^ tu »J cos l; dx = sin l; JsinAT (2) Функция в правой части этого уравнения называется логарифмической функцией.
- Пока что это определяется только для положительных значений x. Далее предположим, что x отрицательно. Тогда -x положительна, поэтому 1n (-x) определено. но Так что, если х отрицателен §- £ = s (s). (3)
Уравнения (2) и (3) могут быть объединены в следующие уравнения: | § = 1n (± *) = 1n | * |, (4) Людмила Фирмаль
| Теорема о среднем | Многочлены |
| Интегрирование | Дробно-рациональные функции |
Примеры решения, формулы и задачи
| Решение задач | Лекции |
| Расчёт найти определения | Учебник методические указания |
- Знак должен быть выбран так, чтобы zhx был положительным. Эти формулы применяются ко всем действительным значениям x, кроме 0. Основной характеристикой In x является Ch. IX выражается отношениями В I = 0, 111 — 111 x, В xy = В X -f В y, Из них вторым является первый и третий очевидные результаты.
Для целей этой главы эти свойства по существу не нужны, но могут быть полезны время от времени, так как некоторые выражения могут быть записаны в более компактной форме с помощью. Из последней характеристики логарифмической функции \ nx * равно 2 1pl%, если l:> 0, и 2 In (-jc>, если l: <0, поэтому в каждом случае 2 In jx | Следовательно, (4) эквивалентно (5) Уравнения (1) — (5) относятся к числу основных уравнений для интегрального расчета.
Вы можете добавить две вещи: J Людмила Фирмаль

