Пример №4. Задача планирования производства.
Для производства трех различных видов деталей используют токарные, фрезерные и строгальные станки. Обработку каждой детали можно вести тремя различными технологическими способами. В табл. 1.2 указаны ресурсы (ч) каждой группы станков и время (ч), затрачиваемые на обработку детали по соответствующему технологическому способу. Прибыль от продажи деталей не зависит от способа производства и составляет 16, 18, 30 единиц за одну деталь первого, второго и третьего вида соответственно. Спланировать производство деталей, обеспечивающее максимум прибыли.
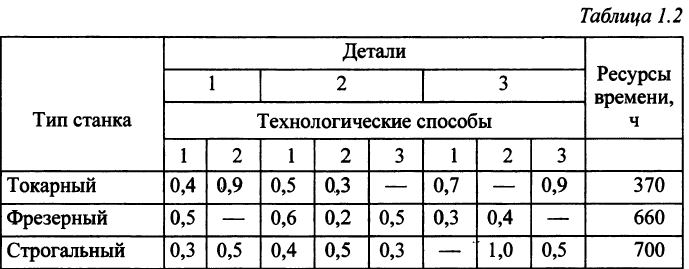
Описание неизвестных. Нужно определить, сколько деталей необходимо изготовить по каждому технологическому способу. Для описания неизвестных мало одного индекса. Нужно указать, во-первых, номер детали, и, во-вторых, номер технологического способа, по которому деталь изготовляется. Обозначим через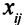 
количество деталей 
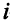-го вида, изготовленных по 
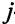-му технологическому способу, 
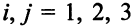. Заметим, что 
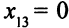, ведь по условию задачи третий способ не применяется для изготовления деталей первого вида. Поэтому имеем всего 8 переменных:
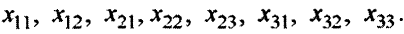
Описание целевой функции. Требуется обеспечить максимум суммарной прибыли. Целевая функция
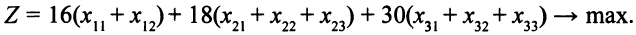
Описание системы ограничений. Необходимо вычислить время, затраченное на обработку на каждом из типов станков всех видов деталей, и потребовать, чтобы это время не превысило имеющихся ресурсов. Например, на производство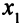 
деталей первого вида по первому технологическому способу требуется 0,4 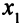часов времени работы токарного станка; на производство 
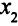деталей первого вида по второму технологическому способу требуется 0,9 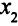часов времени работы токарного станка. Всего же токарные станки должны проработать
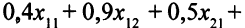
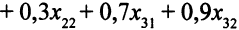
часов. Ограничение по ресурсам времени токарных станков таково:
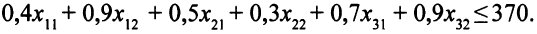
Аналогично строятся ограничения по ресурсам времени фрезерных и строгальных станков:
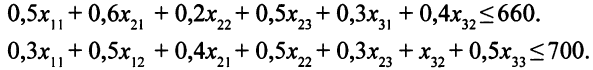
И здесь все переменные не могут быть меньше нуля:
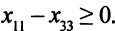
Кроме того, нужно ввести требование целочисленности переменных.
Эта задача взята со страницы решения задач по предмету «линейное программирование»:
Решение задач по линейному программированию
Возможно эти страницы вам будут полезны:
| Пример №2. Задача о раскрое. |
| Пример №3. Задача о смеси. |
| Пример №5. Транспортная задача. |
| Пример №6. Минимизация дисбаланса на линии сборки. |
