Оглавление:












Задача об обтекании полубесконечной пластинки несжимаемой жидкостью
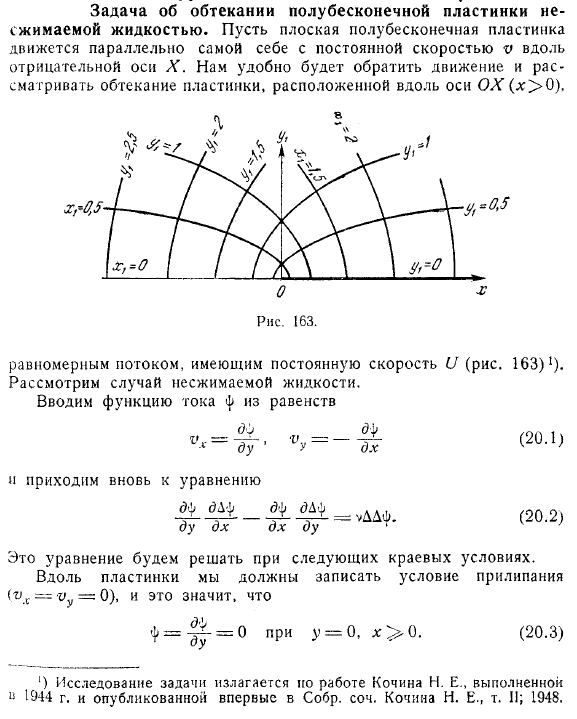
Задача об обтекании полубесконечной пластинки несжимаемой жидкостью. Перевести плоскую полубесконечную пластину с постоянной скоростью v вдоль отрицательной оси x. It полезно обратить движение вспять и рассмотреть обтекание пластин, расположенных вдоль оси ox (x> 0). (Рисунок 163) 1) с равномерным потоком постоянной скорости. Рассмотрим случай несжимаемых жидкостей.
Смотрите также:
Введем функцию потока из равенства (20. 1) И снова приходим к уравнению.Решите это уравнение при следующих граничных условиях: Вдоль пластины необходимо записать условия склеивания (r«vy = 0). Это. . = — — =0 для y-0, x> 0 .(20 .3 ’) Исследование проблемы описано подробно, оно было завершено с 1 44 и было опубликовано впервые в СОБР Н .это объясняется исследованием Кочина . В бесконечности существуют условия (20 .4).
Смотрите также:
В основе решения подобных задач лежит теория пограничного слоя, которая впервые была предложена Л. Прандтлем более века назад. Людмила Фирмаль
Для решения задачи переходим в координатах x, y к параболическим координатам xx, y1, используя следующее соотношение. Кроме того, линия U != 0 вырождается в 2 проходимых отрезка действительной оси от x = 0 до x = + co .Преобразование, показанное в предыдущем разделе, можно использовать для перехода к новой переменной в выражении (20 .2) .(18 .3). Кроме того, это уравнение по (18 .7) (20 .2) можно записать в следующем виде.
Смотрите также:
Плоское течение между двумя пластинками.
Теперь установим граничные условия для пластин, соответствующих линии y*| .=0 .Таким образом, до (20 .3) для y= 0: φ= 0| / = 0 .При удалении от пластины скорость стремится к нулю .Снять с плиты соответствует желанию от уха до уха . Разделите это равенство на ухо и направьте ухо на со, принимая во внимание . Этот ряд можно рассматривать только при больших значениях xx%; его сходимость сомнительна, но его можно рассматривать как асимптотический ряд .
После присвоения (20 .9) (20 .6) функциям/ 0, / x, / 2, .. Для определения равной степени xx>Терма соберите Обыкновенное дифференциальное уравнение рекурсивной системы. Далее справа находится независимая переменная yx, функция/ 0, / x,. .п .содержит X и их производные до 4-го порядка .Решение Хоя обусловлено следующим:необходимо определить нелинейное уравнение (20 .10) до 0 .
Как только вы нашли / 0, вы можете перейти к определению/x из линейного (но относительно/) уравнения справа, которое зависит от коэффициента и / 0 .Затем коэффициенты зависят от/ 0 и определяют линейное уравнение с/ 0, Д и т . д .справа (для/ 2) к/ 2 .Функции/ 0, /, , .. Граничное условие/ » (°) «=/; Д°) =° ’ n = 2. 3,. .(20 .14 Примените правило Допитала, чтобы записать условие (20. 15) в виде /; (со) = 2У, /; (ОО) = 0. (20. 16
Уравнение (20.18) известно как уравнение Блаэнуса. Оно впервые было исследовано в 1908 г. при решении задачи о пограничном слое, с теми же краевыми условиями, что и в данной задаче. Людмила Фирмаль
Перейдем к решению уравнения (20. 10). Прежде всего, следует отметить, что вы можете написать: — Б / О / О) = 0 (20. 17 Таким образом, 1 интеграция возможна. После этой интеграции + (20. 18 (Константа интегрирования выбирается равной нулю, что гарантирует затухание f по отношению к os). Уравнение (20. 18) — это название уравнения Бреннера, известного в гидродинамике literature.
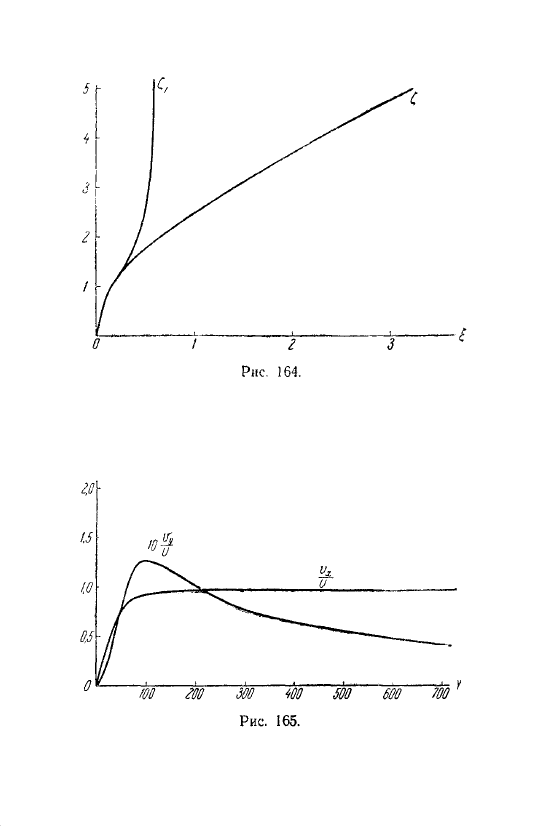
Он впервые был исследован в 1908 году при решении задачи о пограничных слоях (см. § 32 ниже). Чтобы изучить это уравнение, перейдем к безразмерному Функция c и условие безразмерная координата 5. Рассчитаем решение по формуле (20. 20) Вы также можете использовать следующее С » (0) = а. (20. 22) Затем мы последовательно дифференцируем уравнения (20. 20) и используем условие (20. 21), которое можно легко найти . Применяя уравнение Лейбница к равенству (20. 20), его легко обнаружить.

