Равновесие нити

Равновесие нити

Задача о равновесии нити очень распространена в инженерной практике. С ней связаны вопросы определения натяжений электрических проводов, цепей висячих мостов, тросов канатных дорог и т. д. Вместе с тем многие прикладные задачи механики нити не имеют теоретического решения до настоящего времени. Особенно большие затруднения вызывают задачи динамики нити, имеющие большое прикладное значение, например в текстильной промышленности.

Механикой нити стали заниматься сразу же после открытия дифференциального исчисления. И. Бернулли изучал равновесие

тяжелой однородной нити и установил форму цепной линии. Дальнейшее развитие механики нити связано с именами Эйлера, Резаля, Кельвина, Рауса.

Уравнения равновесия

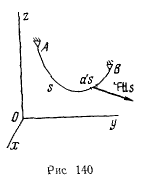
Рассмотрим задачу о равновесии гибкой нерастяжимой и несжимаемой нити длиной I, закрепленной своими концами в неподвижных точках А и В (рис. 140), на которую действуют непрерывно распределенные силы. Под нитью будем понимать систему материальных точек, сплошь покрывающих некоторую линию. В действительности всякая нить имеет толщину, но в тех случаях, когда длина нити достаточно велика по сравнению с толщиной, влиянием толщины можно пренебрегать. Обозначим через р линейную плотность нити, т. е. отношение массы какого-либо элемента нити к его длине. Если обозначить элемент массы через dm а элемент длины через ds, то плотность выразится в виде

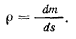
Обозначим через s длину дуги нити, отсчитываемую от какого-либо начала в определенном направлении. Для определенности примем за начало точку А и положительным будем считать направление от точки А к точке В вдоль нити. Выделяя на нити элемент ds, будем предполагать, что внешние силы, действующие на этот элемент, можно представить одной силой Fds, приложенной в некоторой точке элемента. Проекции этой силы на неподвижные оси координат равны 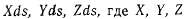— проекции вектора F, который назовем силой, отнесенной к единице длины. Пренебрегая размерами элемента ds, будем рассматривать его как одну материальную точку с массой dm, находящуюся под действием силы Fds, связанную с соседними элементами. Координаты этой точки обозначим через х, у, z, а ее возможные перемещения через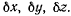

Чтобы из принципа возможных перемещений получить уравнения равновесия нити, нужно вычислить сумму работ всех активных сил на произвольном возможном перемещении всей нити, принимая во внимание, что возможные перемещения стеснены условием нерастяжимости и несжимаемости нити. Для этой цели можно использовать метод неопределенных множителей Лагранжа. Элементарная работа силы Fds, действующей на элемент ds, на возможном перемещении элемента имеет вид

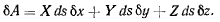
Сумма элементарных работ

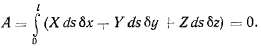
Условия связи, накладываемые на возможные перемещения элемента ds нерастяжимостью и несжимаемостью элемента, запишутся в виде равенства

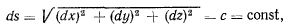
откуда

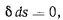
или, если обозначить

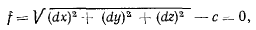
получим

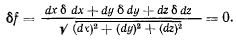
Умножая это уравнение на неопределенный множитель 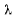и интегрируя по длине нити, будем иметь

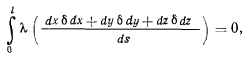
где множитель 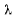является функцией s и имеет свое особое значение для каждого элемента ds. Складывая (а) и (b), запишем условие Лагранжа

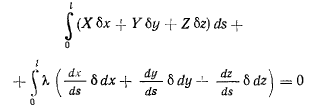
На концах нити возможные перемещения удовлетворяют следующим условиям:

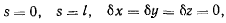
причем справедливы равенства

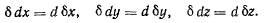
В самом деле, рассматривая координаты х, у, z элемента ds как функции длины дуги s, с точностью до малых второго порядка будем иметь

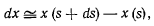
тогда

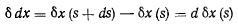
и уравнение (с) можно будет переписать в виде

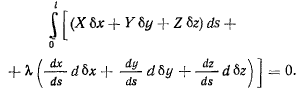
Интегрируя по частям

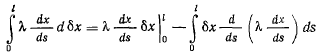
и принимая во внимание, что 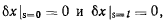получим

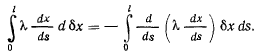
Аналогичные формулы имеют место для у и z. После такого преобразования уравнение (d) перепишется в виде

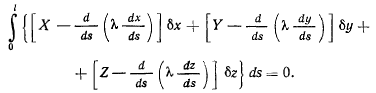
Чтобы отсюда получить уравнения равновесия, следуя методу Лагранжа, необходимо приравнять нулю коэффициенты при 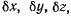т. е. положить

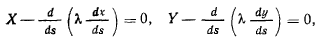
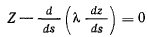
в каждой точке нити. Полученные уравнения являются уравнениями равновесия нити с множителями Лагранжа. После исключения из этих уравнений 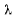получим уравнение кривой, определяющей форму нити при ее равновесии.

Переписывая уравнение (е) в виде

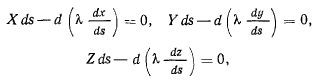
заметим, что вторые части этих уравнений представляют собой равнодействующую сил реакций, действующих на элемент ds со сто-

роны соседних элементов. Для идеально гибкой нити такими силами реакции являются только силы натяжения нити 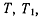направленные вдоль нити (рис. 141). Сумма проекций этих сил на ось х имеет вид

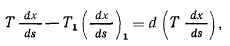
где 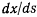— косинус угла между положительным направлением оси х и положительным направлением касательной к нити. Сравнивая это уравнение с (f), получим

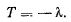
Отсюда видно, что множитель 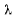определяет силу натяжения нити, а уравнения равновесия нити можно представить в виде

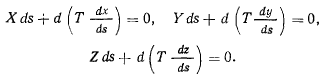
Естественные уравнения равновесия нити

С элементом ds нити в некоторой ее точке М свяжем систему прямоугольных осей, определяемую единичными векторами 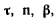(рис. 142), первый из которых направлен по касательной к нити в точке M, второй — по главной нормали, третий — по бинормали. Обозначим направляющие косинусы касательной через 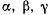направляющие косинусы нормали — через 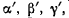направляющие косинусы бинормали — через 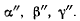— Тогда уравнения равновесия нити (g) можно будет записать в виде

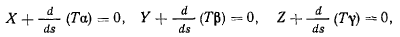
или, воспользовавшись формулами Френе — Серре

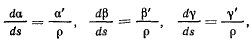
в виде

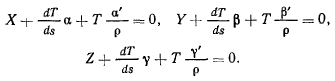
Умножая каждое из этих уравнений соответственно на 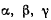и складывая, получим

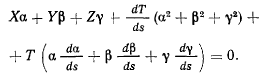
Здесь первая сумма

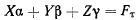
представляет проекцию силы, отнесенной к единице длины нити, на касательную к нити в точке М. Имея в виду соотношения

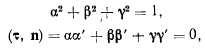
перепишем полученное выше уравнение в виде

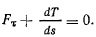
Умножая каждое из уравнений (h) соответственно на 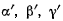и складывая, получим

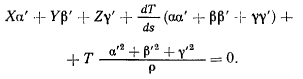
Первая часть этого уравнения представляет проекцию силы, отнесенной к единице длины, на главную нормаль. Принимая во внимание соотношение

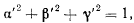
получим

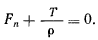
Умножая далее уравнения (h) соответственно на 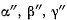и складывая, будем иметь

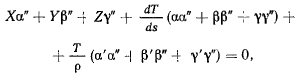
откуда находим

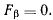
Полученные уравнения

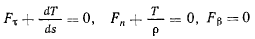
являются уравнениями равновесия нити в проекциях на естественные оси координат, или естественными уравнениями равновесия нити. Из первого уравнения (i) имеем

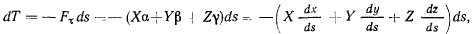
или

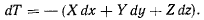
Если силы допускают существование силовой функции, то последнее уравнение перепишется в виде

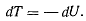
Интегрируя это соотношение, получим

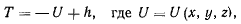
т. с. при наличии силовой функции натяжение нити в произвольной точке М полностью определяется через координаты этой точки.

Зная форму нити и натяжение в некоторой точке, можно определить натяжение в любой другой точке нити.

Пример:

Исследовать положение равновесия нити, к точкам которой приложены параллельные силы.

Решение:

Предположим, что силы параллельны оси г. Тогда уравнения (g) приобретают вид

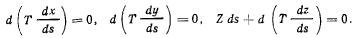
Интегрируя первые два уравнения, получим

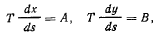
где А и В — произвольные постоянные. Разделив второе из полученных равенств на первое, будем иметь

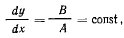
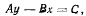
где С — новая произвольная постоянная. Этому уравнению плоскости должны удовлетворять координаты всех точек нити, т. е. нить принимает форму плоской кривой.

Пример:

Определить форму равновесия тяжелой однородной нити, закрепленной d двух произвольных точках А и В.

Решение:

Силы тяжести — параллельные силы, а потому нить будет расположена в вертикальной плоскости, проходящей через точки А и В (рис. 143). Выберем систему прямоугольных осей Аху с началом в точке А так, чтобы ось х была расположена в плоскости нити горизонтально, а ось у направлена вертикально вверх. Координаты точки В обозначим через а и b. Тогда уравнения равновесия (£) запишутся в виде

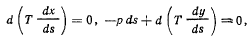
где р — вес единицы длины ннтн. Интегрирование первого из этих уравнений дает

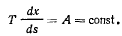
Будем предполагать, что 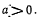Тогда 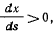а значит» и 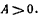Подставляя найденное отсюда значение Т в последнее из уравнений (k), получим

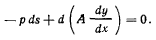
Здесь дифференциал дуги

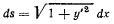
и, вводя обозначение 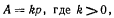будем иметь

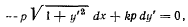
или

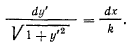
Интегрируя это уравнение, получим

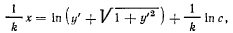
или

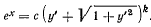
Обозначая через 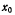координату x точки нити, в которой касательная к нити горизонтальна, так что при 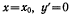следовательно, 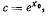будем иметь

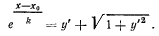
Представим это уравнение в виде

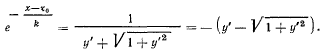
Вычитая второе уравнение из первого, будем иметь

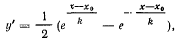
откуда, интегрируя, получим

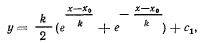
где 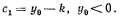Если ввести новые координаты

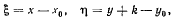
то последнее уравнение приобретет вид

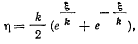
или

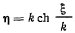
Последнее уравнение характеризует связь между координатами 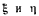и представляет уравнение кривой, по которой располагается нить при равновесии. Эта кривая симметрична относительно оси 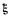и называется цепной линией. Ось 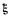называется направляющей цепной линии, а расстояние к самой нижней точки нити от оси 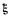называется параметром цепной линии.

Для определения натяжения нити можно воспользоваться уравнением

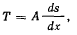
откуда

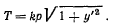
Подставляя сюда значение 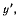находим

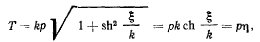
т. е.

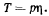
Отсюда видно, что натяжение нити возрастает пропорционально ординатам, если за ось 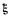взята направляющая цепной линии. Если представить, что ординаты — материальные прямые, сделанные из той же нити, то можно сказать, что натяжение в каждой точке нити равно весу соответствующей ординаты. Уравнение цепной линии

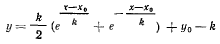
содержит три параметра 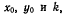которые могут быть определены из условий на концах нити. В самом деле, пусть точка В расположена выше точки А Тогда в точке 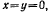и, следовательно,

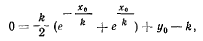
или

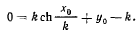
В точке 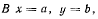откуда

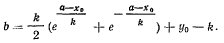
Определяя длину нити

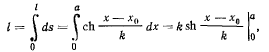
имеем

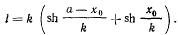
Полученные уравнения позволяют определить три параметра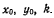

Покажем, что существует единственное положение равновесия нити Для этого предварительно, вводя обозначение 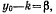перепишем полученные уравнения в виде

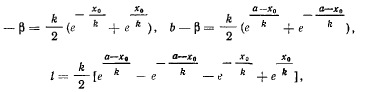
откуда

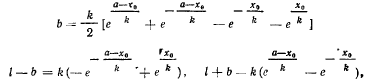
Перемножая два последних уравнения, получим

где 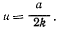При 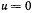выражение 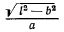обращается в единицу, а

при возрастании а также неограниченно возрастает, т. е. при равновесии

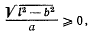
или

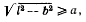
откуда

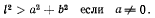
Последнее условие означает, что длина нити больше расстояния между точками А и В. Если это условие выполнено, то можно определить и, и для постоянных 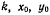получается одна единственная система значении, т. е. существует одно положение равновесия.

Пример:

Определить условия равновесия гибкой нити, находящейся под действием центральных сил (силы, линии действия которых проходят через одну неподвижную точку —центр сил).

Решение:

В рассматриваемом случае момент силы, действующей на элемент нити ds, относительно любой оси, проходящей через центр сил, равен нулю. Принимая за начало прямоугольной системы осей Oxyz центр сил, будем иметь

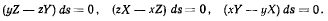
Умножая соответствующие уравнения равновесия нити (g) на х, у, z и складывая, получим

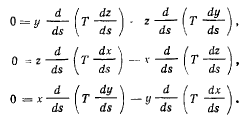
Переписывая эти уравнения в виде

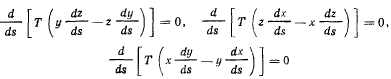
и интегрируя их, получим

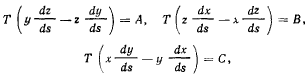
где А, В и С — произвольные постоянные. Умножая первое из полученных уравнений на х, второе на у, третье на z и складывая, находим

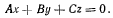
Полученное уравнение является уравнением плоскости, проходящей через начало координат, которому удовлетворяют координаты всех точек нити, т. е. при равновесии нить имеет фигуру плоской кривой.

Примем плоскость, в которой расположена нить, за плоскость Оху. Тогда 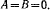Введем полярные координаты

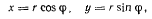
тогда

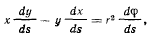
и последний интеграл перепишется к виде

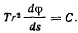
Предположим, что силы, действующие на нить, зависят только от координат точек приложения сил и обладают силовой функцией. Тогда из уравнения (j) будем иметь

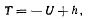
и задача сводится к квадратурам, В самом деле, дифференциал дуги в полярных координатах равен

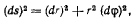
поэтому интеграл можно записать в виде

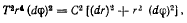
или

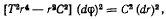
откуда

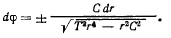
Определив из (j’) T как функцию r и подставив в полученное уравнение, наедем уравнение с разделенными переменными, определяющее форму равновесия нити.

Эта лекция взята со страницы, где размещены все лекции по предмету теоретическая механика:

Предмет теоретическая механика

Эти страницы возможно вам будут полезны:

Определение реакций связи

Определение реакции связи в общем случае

Основные законы динамики

Две основные задачи динамики