Пример №2. Задача о раскрое.
Для изготовления брусьев трех длин (0,2; 0,3 и 0,5 м) на распил поступили бревна длиной 1 м. Нужно получить не менее 150 и не более 200 брусьев длиной 0,2 м; не менее 200 и не более 300 брусьев длиной 0,3 м; не менее 300 и не более 330 брусьев длиной 0,5 м. Как распиливать бревна, чтобы обеспечить нужное число брусьев каждого размера и при этом минимизировать отходы?
Прежде всего опишем все способы распила одного бревна. Например, бревно длиной 1 м можно распилить на 5 брусьев длиной 0,2 м, отходов в этом случае нет. Или можно получить 3 бруса длиной 0,3 м, тогда в отходы уйдет 0,1 м бревна. Варианты распила приведены в табл. 1.1.
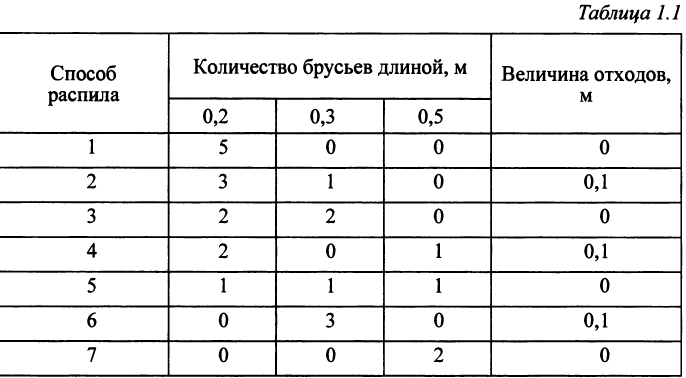
Опишем математическую модель задачи.
Описание неизвестных. Неизвестно, сколько бревен следует распиливать каждым из способов, указанных в табл. 1.1. Обозначим через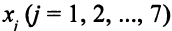 
количество бревен, распиленных 
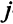-м способом. Всего 7 неизвестных, каждое из них может принимать только целые значения: 0,1,2, 3,….
Описание целевой функции. Требуется минимизировать суммарные отходы. Отходы остаются только в случае применения 2,4, 6-го способов. Если распил одного бревна дает единицу отходов (0,1 м), то распил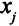 
бревен дает 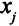единиц отходов. Суммарная величина отходов равна
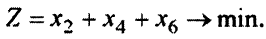
Описание системы ограничений. Всего брусьев длиной 0,2 м будет получено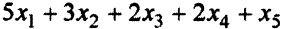 
штук (6-й и 7-й способы распила не дают брусьев длиной 0,2 м). По условию число брусьев длиной 0,2 м должно лежать в пределах от 150 до 200, получаем два ограничения:
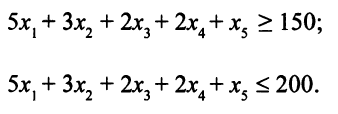
Аналогично строятся ограничения по числу брусьев длиной 0,3 м и длиной 0,5 м.
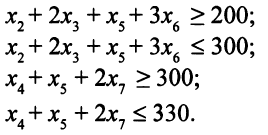
Добавим также условие неотрицательности и целочисленности переменных:
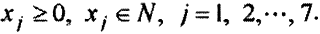
Изменим теперь условие задачи. Пусть требуется получить ровно 150 брусьев длиной 0,2 м, 200 брусьев длиной 0,3 м, 300 брусьев длиной 0,5 м и при этом минимизировать суммарные отходы.
Пусть снова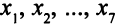 
— количество бревен, распиленных по 1-му, 2-му, …, 7-му способам соответственно. Тогда количество брусьев длиной 0,2; 0,3 и 0,5 м будет соответственно таким:
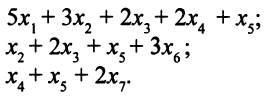
Так как переменные 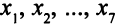принимают только целые значения, нельзя гарантировать, что в результате распила получится, например, ровно 150 брусьев длиной 0,2 м. Можно потребовать только, чтобы их было не меньше 150 штук. Но если их будет, например, 152 штуки, получится еще 0,4 дополнительных единиц отходов. Обозначим через 
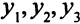избыточные количества брусьев длиной 0,2; 0,3; 0,5 м. Они привнесут в целевую функцию дополнительно 
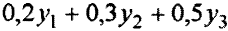единиц отходов.
Окончательно целевая функция выглядит так:
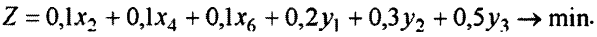
Система ограничений примет вид:
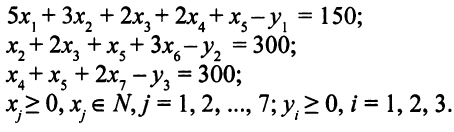
Эта задача взята со страницы решения задач по предмету «линейное программирование»:
Решение задач по линейному программированию
Возможно эти страницы вам будут полезны:
| Пример №30. Найдем максимальный поток в сети, показанной на рис. 8.2. |
| Пример №1. Задача распределения ресурсов. |
| Пример №3. Задача о смеси. |
| Пример №4. Задача планирования производства. |
