Оглавление:
Задача о назначениях (проблема выбора)
Будем рассматривать задачу о распределении механизмов (работников) на 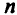 видов работ таким образом, чтобы каждый механизм (работник) выполнял только одну работу и чтобы при заданной производительности каждого механизма на каждой из работ суммарный эффект был максимальным.
видов работ таким образом, чтобы каждый механизм (работник) выполнял только одну работу и чтобы при заданной производительности каждого механизма на каждой из работ суммарный эффект был максимальным.
Пусть 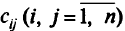 — производительность
— производительность 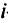 -го механизма на
-го механизма на 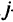 -й работе. Тогда данная задача, известная под названием задачи о назначениях, будет заключаться в таком выборе по одному элементу матрицы
-й работе. Тогда данная задача, известная под названием задачи о назначениях, будет заключаться в таком выборе по одному элементу матрицы 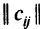 из каждой строки и каждого столбца, чтобы их сумма
из каждой строки и каждого столбца, чтобы их сумма
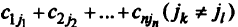
при 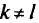 была максимальной.
была максимальной.
Обозначив через 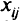 переменную, равную единице, если
переменную, равную единице, если 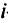 -й механизм назначен на
-й механизм назначен на 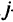 -ю работу, и нулю, если он на эту работу не назначен, мы сведем задачу к следующей задаче линейного программирования.
-ю работу, и нулю, если он на эту работу не назначен, мы сведем задачу к следующей задаче линейного программирования.
Среди неотрицательных целочисленных решений системы 2 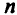 уравнений
уравнений
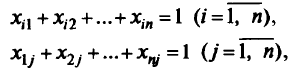
означающих, что каждый механизм выполняет одну работу и каждая работа обеспечивается одним механизмом, найти то, которое максимизирует
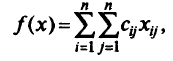
означающее суммарную производительность всех механизмов. Эту задачу решают с помощью сетевых методов, менее громоздких, чем симплекс-метод (см. гл. 3).
Пример:
Имеются три механизма 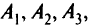 каждый из которых может быть использован на каждом из трех видов работ
каждый из которых может быть использован на каждом из трех видов работ 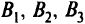 с производительностью (в условных единицах), заданной в виде следующей таблицы.
с производительностью (в условных единицах), заданной в виде следующей таблицы.
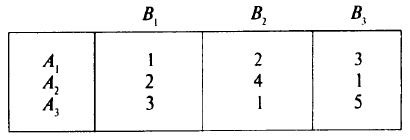
Требуется так распределить механизмы по одному на каждую из работ, чтобы суммарная производительность всех механизмов была максимальной.
Обозначим, как рекомендовалось выше, через 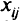 переменную, равную единице, если механизм
переменную, равную единице, если механизм 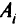 назначен на работу
назначен на работу 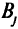 и равную нулю, если механизм
и равную нулю, если механизм 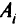 не назначен на работу
не назначен на работу 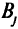 . Тогда суммарная производительность механизмов
. Тогда суммарная производительность механизмов
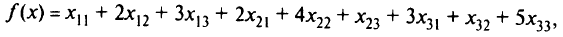
при ограничениях
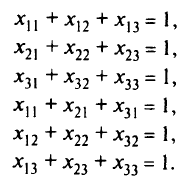
Надо максимизировать 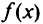 при этих ограничениях.
при этих ограничениях.
Переписав ограничения задачи в виде 0-уравнений, составим таблицу
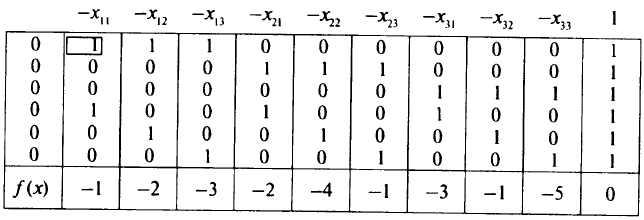
После избавления от нулевых строк и вычеркивания столбцов, расположенных под перенесенными наверх нулями, получим таблицу

Среди свободных членов таблицы есть отрицательный, так что опорное решение еще не получено.
Сделав шаг метода исключения Жордана (разрешающий элемент-1 отмечен), получим таблицу
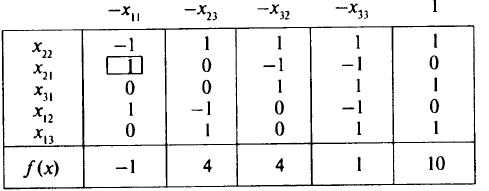
В ней все свободные члены неотрицательны, поэтому можно перейти к отысканию оптимального решения. Выбрав разрешающий элемент, как указано в таблице, и сделав один шаг модифицированного жорданова исключения, получим окончательно
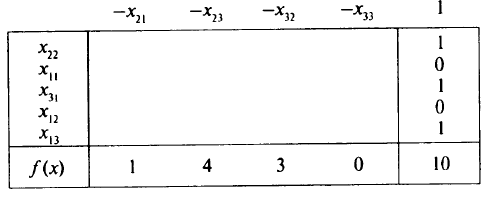
Из последней таблицы следует, что максимальная суммарная производительность всех механизмов равна 10 (условным единицам) и достигается при
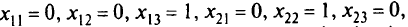
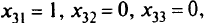
т.е. при назначениях механизмов 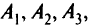 , соответственно на работу
, соответственно на работу 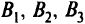 .
.
Так как в 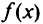 -строке последней таблицы есть нулевой элемент, то полученное оптимальное решение задачи не единственное. Сделав шаг модифицированного жорданова исключения с разрешающим элементом из столбца, содержащего нуль в
-строке последней таблицы есть нулевой элемент, то полученное оптимальное решение задачи не единственное. Сделав шаг модифицированного жорданова исключения с разрешающим элементом из столбца, содержащего нуль в 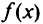 -строке, можно найти другое оптимальное решение этой же задачи.
-строке, можно найти другое оптимальное решение этой же задачи.
Эта теория взята со страницы лекций по предмету «математическое программирование»:
Предмет математическое программирование
Возможно эти страницы вам будут полезны:

