Не для всякой функции можно вычислить определенный интеграл с помощью известных нам способов. Кроме того, на практике часто сталкиваются с функциями, заданными табличным и графическим способами, или с функциями, интегралы от которых выражаются через очень громоздкие функции. В этих случаях вычисления по формуле Ньютона-Лейбница либо невозможны, либо затруднительны, поэтому прибегают к различным методам приближенного (численного) интегрирования.
Рассмотрим функцию 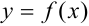 , непрерывную на отрезке
, непрерывную на отрезке 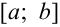 и для наглядности
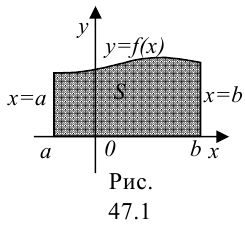
и для наглядности 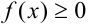 . Тогда в силу геометрического смысла определенного интеграла, он численно равен площади криволинейной трапеции, ограниченной графиком функции
. Тогда в силу геометрического смысла определенного интеграла, он численно равен площади криволинейной трапеции, ограниченной графиком функции 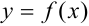 , прямыми
, прямыми 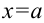 и
и 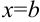 , отрезком
, отрезком 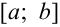 оси
оси 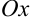 , т.е.
, т.е. 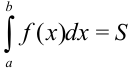 (рис. 47.1).
(рис. 47.1).
Основная задача методов численного интегрирования заключается в том, чтобы как можно точнее найти площадь фигуры 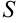 . Это число как раз и будет являться приближенным значением определенного интеграла.
. Это число как раз и будет являться приближенным значением определенного интеграла.
Эта лекция взята с главной страницы на которой находится курс лекций с теорией и примерами решения по всем разделам высшей математики:
Другие лекции по высшей математике, возможно вам пригодятся:
| Метод хорд. |
| Метод касательных. |
| Формулы прямоугольников. |
| Формула трапеций. |
