Задача C2. Ракета стартовала с земли вертикально вверх, двигаясь равноускоренно с ускорением 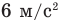 . Через 10 с двигатель ракеты заглох. Через сколько времени она упадет на землю? Сопротивлением воздуха пренебречь.
. Через 10 с двигатель ракеты заглох. Через сколько времени она упадет на землю? Сопротивлением воздуха пренебречь.
Обозначим 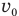 — скорость ракеты на старте, а — ускорение при взлете,
— скорость ракеты на старте, а — ускорение при взлете, 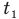 — время равноускоренного движения, g — ускорение свободного падения, v — скорость в высшей точке подъема, t — все время полета ракеты,
— время равноускоренного движения, g — ускорение свободного падения, v — скорость в высшей точке подъема, t — все время полета ракеты, 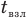 — время взлета до высшей точки,
— время взлета до высшей точки, 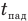 — время свободного падения с высшей точки до земли,
— время свободного падения с высшей точки до земли, 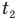 — время равнозамедленного движения вверх до высшей точки подъема после выключения двигателей, h — всю высоту, на которую взлетела ракета,
— время равнозамедленного движения вверх до высшей точки подъема после выключения двигателей, h — всю высоту, на которую взлетела ракета, 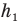 — высоту равноускоренного подъема,
— высоту равноускоренного подъема, 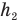 — высоту равнозамедленного подъема.
— высоту равнозамедленного подъема.
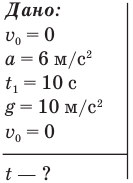
Решение:
Сразу понятно, что все время t от старта до падения ракеты на землю можно представить только как сумму двух разных времен: времени взлета 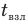 времени падения
времени падения 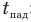 :
:
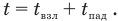
Следует сообразить, что время взлета складывается из времени 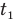 , в течение которого ракета взлетала вверх с ускорением а, т.е. набирала скорость, пока у нее не заглох двигатель, и времени
, в течение которого ракета взлетала вверх с ускорением а, т.е. набирала скорость, пока у нее не заглох двигатель, и времени 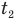 , в течение которого она продолжала двигаться вверх уже замедленно, с отрицательным ускорением свободного падения. Эту часть подъема ракета проделала с начальной скоростью, которую она приобрела к моменту, когда двигатель заглох, пока не достигла высшей точки. Следовательно, все время взлета
, в течение которого она продолжала двигаться вверх уже замедленно, с отрицательным ускорением свободного падения. Эту часть подъема ракета проделала с начальной скоростью, которую она приобрела к моменту, когда двигатель заглох, пока не достигла высшей точки. Следовательно, все время взлета
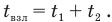
Давайте сначала найдем скорость 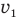 которую ракета набрала к моменту, когда у нее заглох двигатель. Эту скорость можно найти по формуле скорости равноускоренного движения при нулевой начальной скорости на старте. Тогда эта формула приобретет вид:
которую ракета набрала к моменту, когда у нее заглох двигатель. Эту скорость можно найти по формуле скорости равноускоренного движения при нулевой начальной скорости на старте. Тогда эта формула приобретет вид:
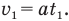
Эта скорость станет начальной скоростью для движения ракеты в течение времени 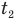 с отрицательным ускорением свободного падения -g до высшей точки подъема, где ее конечная скорость v станет равна нулю. Поэтому для нахождения времени
с отрицательным ускорением свободного падения -g до высшей точки подъема, где ее конечная скорость v станет равна нулю. Поэтому для нахождения времени 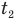 можно применить ту же формулу скорости:
можно применить ту же формулу скорости:
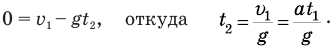
Подставив (3) в (2), выразим время взлета через все известные величины:
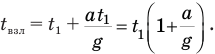
Теперь надо найти время падения ракеты с высшей точки ее подъема на землю. Проще всего это можно было бы сделать, если бы нам была известна вся высота подъема ракеты h. Время падения с этой высоты мы обозначили 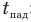 , поэтому формула высоты примет вид:
, поэтому формула высоты примет вид:
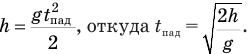
Значит, надо определить всю высоту h подъема ракеты — от старта до высшей точки, где она остановилась, после чего стала падать. Готовой формулы для ее определения нет, ведь эта высота представляет собой сумму двух высот 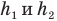 с разными типами движения: при подъеме на высоту
с разными типами движения: при подъеме на высоту 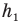 — равноускоренного с ускорением а и при подъеме на высоту
— равноускоренного с ускорением а и при подъеме на высоту 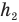 — равнозамедленного с отрицательным ускорением свободного падения — g. Поэтому мы должны записать:
— равнозамедленного с отрицательным ускорением свободного падения — g. Поэтому мы должны записать:
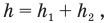
где
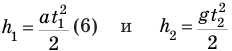
или с учетом равенства (3)
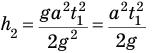
Тогда с учетом равенств (6) и (7) вся высота подъема ракеты будет равна:
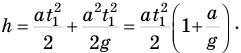
Нам остается подставить правую часть этого равенства в формулу (5) и сложить времена взлета и падения. Приступим:
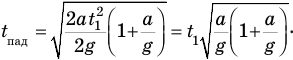
Теперь подставим правые части равенств (4) и (9) в формулу (1), и задача будет решена:
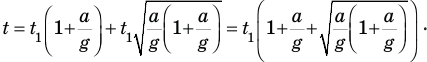
Задача в общем виде решена. Подставим числа и вычислим:
Ответ: 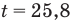 с.
с.
Эта задача взята со страницы подробного решения задач по физике, там расположена теория и подробное решения задач по всем темам физики:
Возможно вам будут полезны эти задачи:
