Тип работы: Задача
Предмет: Сопротивление материалов
Статус: Выполнен
Год работы: 2020
Страниц: 1
Оригинальность: 95% (antiplagiat.ru)
Формат: Скан (Рукопись)
Цена: 294 руб.
Как получить работу? Ответ: Напишите мне в whatsapp и я вышлю вам форму оплаты, после оплаты вышлю решение.
Как снизить цену? Ответ: Соберите как можно больше задач, чем больше тем дешевле, например от 10 задач цена снижается до 50 руб.
Вы можете помочь с разными работами? Ответ: Да! Если вы не нашли готовую работу, я смогу вам помочь в срок 1-3 дня, присылайте работы в whatsapp и я их изучу и помогу вам.
Благодаря этой странице вы научитесь сами решать такие задачи:
Другие похожие задачи:
Описание работы:
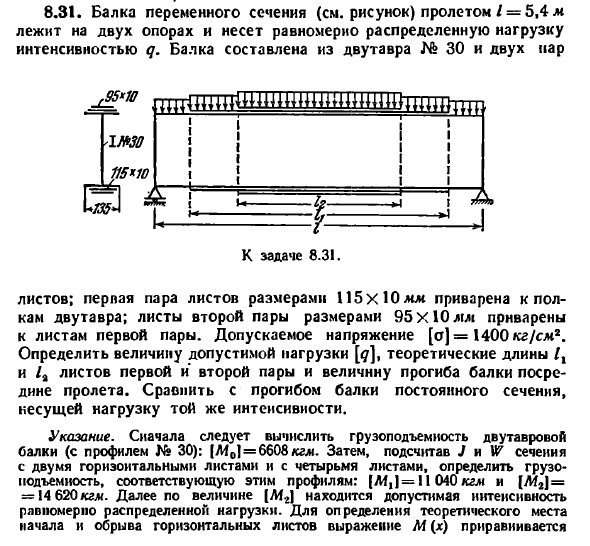
Задача 8.31. Балка переменного сечения пролетом L = 5,4 м лежит на двух опорах и несет равномерно распределенную нагрузку интенсивностью q. Балка составлена из двутавра № 30 и двух пар листов; первая пара листов размерами 115х10 мм приварена к полкам двутавра; листы второй пары размерами 95×10 лип приварены к листам первой пары. Допускаемое напряжение [Q] = 1400 кг/см2. Определить величину допустимой нагрузки [Q], теоретические длины /, и L2 листов первой и второй пары и величину прогиба балки посредине пролета. Сравнить с прогибом балки постоянного сечения, несущей нагрузку той же интенсивности. Указание. Сначала следует вычислить грузоподъемность двутавровой балки (с профилем № 30): |Мо = 6608кгм. Затем, подсчитав J и W сечения с двумя горизонтальными листами и с четырьмя листами, определить грузоподъемность, соответствующую этим профилям: [М,] = 11 040 кгм и [Л*2) = = 14 620 кгм. Далее по величине [М2] находится допустимая интенсивность равномерно распределенной нагрузки. Для определения теоретического места начала и обрыва горизонтальных листов выражение М(х) приравнивается с (Мо) и (М1) Величину прогиба удобно вычислить при помощи теоремы Кастильяно, суммируя три интеграла, по числу участков балки разной жесткости.
