
Тип работы: Задача
Предмет: Сопротивление материалов
Статус: Выполнен
Год работы: 2020
Страниц: 1
Оригинальность: 97% (antiplagiat.ru)
Формат: Скан (Рукопись)
Цена: 291 руб.
Как получить работу? Ответ: Напишите мне в whatsapp и я вышлю вам форму оплаты, после оплаты вышлю решение.
Как снизить цену? Ответ: Соберите как можно больше задач, чем больше тем дешевле, например от 10 задач цена снижается до 50 руб.
Вы можете помочь с разными работами? Ответ: Да! Если вы не нашли готовую работу, я смогу вам помочь в срок 1-3 дня, присылайте работы в whatsapp и я их изучу и помогу вам.
Благодаря этой странице вы научитесь сами решать такие задачи:
Помощь по сопромату и решение задач на заказ
Другие похожие задачи:
| Задача 5.6 Для балки с наклонным участком | Задача 5.9 Для рамы построить эпюры |
| Задача 5.7 Построить эпюры внутренних усилий | Задача 5.10 Для рамы на рис.5.18 построить эпюры |
Описание работы:
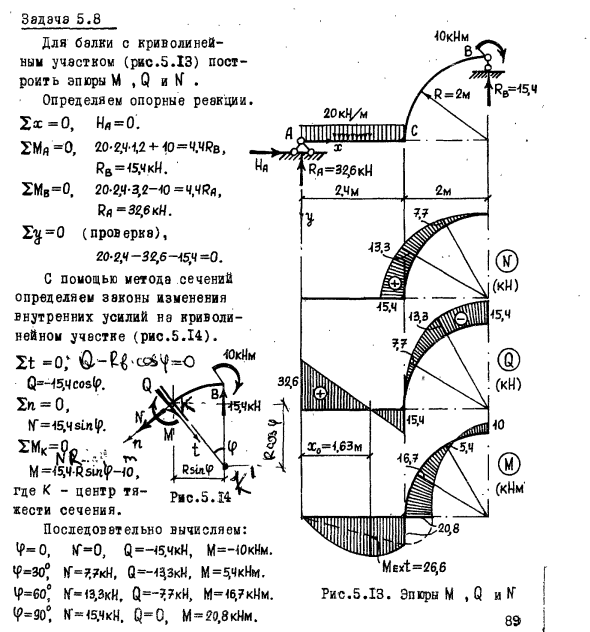
Задача 5.8 Для балки с криволинейным участком (рис.5.13) построить эпюры М , Q и Н . Определяем опорные реакции (проверка), 20-2,4-32,6-15,4=0. С помощью метода сечений определяем законы изменения внутренних усилий на криволинейном участке (рис.5.14). где К — центр тяжести сечения. Последовательно вычисляем: Рис.5.13. Эпюры M , Q На криволинейном участке ВС внутренние усилия меняются по синусоиде. Продольная сила является растягивающей,а изгибающий момент в пределах участка меняет знак. Вычисляем внутренние усилия в характерных сечениях горизонтального участка -АС. Сечение Я ГГ-О, Q = Ра =32,6кН. М=0. Сечение С Q = 32,6 — 20-2,4—адкН, М = 32,6-2,4-20-2.Ч*=20,8кНм (растянуты нижние волокна). Вычисляем значение экстремального момента на участке АС : Q(X) = 32.6 — 20Х =0, На участке М изгибающий момент меняется по закону квадратной параболы. Эпюры внутренних усилий приведены на рис.5.13.
