Оглавление:





Взаимодействие жидкости с телом крылового профиля
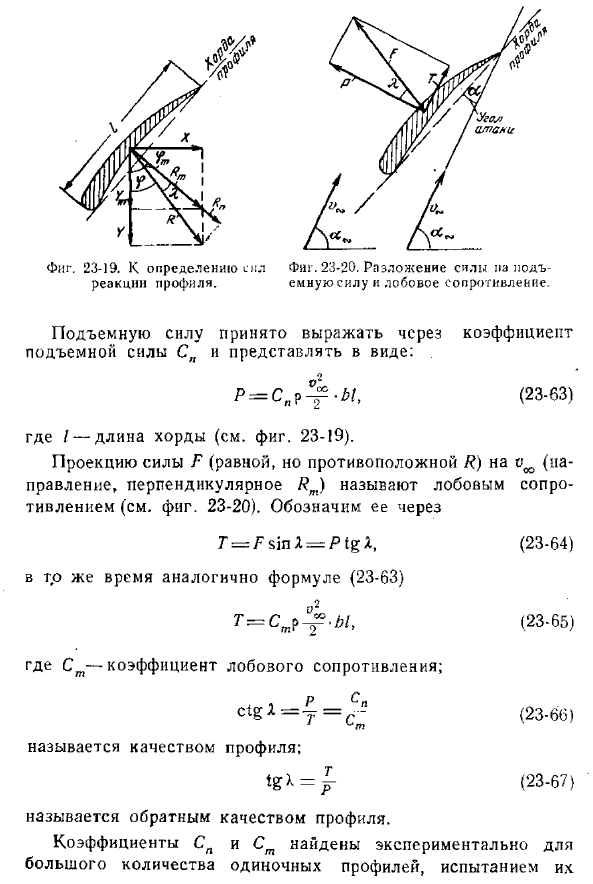
Взаимодействие жидкости с телом крылового профиля. Теорема Н. Е. Жуковского о подъемной силе. Теорема Н. Е. Жуковского об определении подъемной силы основана на гидродинамической теории профиля крыла или крыла гидромеханического крыла, а также на предположении С. А. Чапригина о непрерывном обтекании задней кромки крыла. Эта теорема была опубликована Н. Е. Жуковским в 1906 г., когда работа «О связанном вихре» была применена к одному крылу, а затем распространена на профиль крыла.
Вихревая система крылового профиля индуцирует поле скоростей, которые складываются с однородным набегающим потоком. Людмила Фирмаль
- Та же фигура. 23 * 15. Схема циркуляции потока вокруг обтекаемого объекта. _ ** ^ o Так называемая решетка, профиль Т сюризованной системы Суть этого явления заключается в следующем. Как установлено выше, пограничный слой является источником вихрей, которые ухудшают плавкий поток вокруг тела. Эти вихри являются не только появлением сопротивления давлению, но и причиной так называемой подъемной силы.
Создает движение, которое происходит в потоке и циркулирует вокруг обтекаемого тела (Рис. 23-15), наложенного на основной поток, что приводит к неравномерной скорости с обеих сторон обтекаемого тела, создавая перепады давления и подъемные силы вы. 1 Н, Е. Жуковский, Проц о родственных вихрях. Физические науки Общепринятый естествознание, т. П, пп. 2, 1907; Н. Е. Жуковский, Избранные труды, вып. Г., гос. Дом Тех. Выдано Теор. Литература, 1948, § 23-8] Теорема //. Е. Жуковский 401
- Н. Е. Жуковский заменил сложную систему вихрей пограничного слоя на фиктивные, связанные с исследуемым твердым телом вихрями в обтекаемом теле для определения подъемных сил вокруг тела. Предлагается создать круговое движение. N, E остается в идеальном гидродинамическом каркасе жидкости из-за потенциальной схемы потока с вихрями. Жуковскому удалось доказать следующую теорему для одного крыла.
Давление невихревого потока, который течет по контуру с циркуляцией G со скоростью V, составляет P =? Уорд; ^ 23-46) Это направление силы может быть получено вращением вектора V под прямым углом к противоположному направлению циркуляции. Циркуляция векторов скорости называется интегрированием G C ^ / cosO, (23-47) Получить в любой замкнутой петле (рис. 23-16). Где V скорость частицы в контуре, а 6 угол, который вектор скорости образует с касательной к контуру.
В результате позади тела образуется длинный вихревой след, который обусловливает силу сопротивления при обтекании тонкого крылового профиля. Людмила Фирмаль
- Докажем теорему о решетке. Для этого рассмотрим поток жидкости вокруг системы лопаток (сетки), установленной на равном расстоянии друг от друга I (шаг лопатки) (рисунок 23-17). Окружите одно из лезвий контрольной поверхностью. Поперечное сечение поверхности управления образовано двумя линиями тока на расстоянии шага лопасти 4 и двумя горизонтальными линиями длины I (см. Рисунок 23-17, поверхность управления 26 н. 3. Френкель. 402 Поток жидкости и твердое взаимодействие.
Смотрите также:
Возможно эти страницы вам будут полезны:
- Мощность струи, действующей на поверхности, движущиеся поступательно, прямолинейно и равномерно.
- Индикаторная мощность потока жидкости, действующего на, поверхность, вращающуюся с постоянной угловой скоростью вокруг неподвижной оси.
- Дифференциальное уравнение установившегося безнапорного потока.
- Равномерное движение.

