Взаимный момент системы скользящих векторов

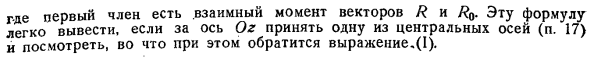
Взаимный момент системы скользящих векторов

• Используя обозначения в разделе 18, взаимные моменты 2 векторных систем 5 и 0 называются величинами + L1G0 4 AG20 b 4 MdUN 2, 1. Его значение не зависит от выбора axes. In факт, эта сумма может быть представлена в следующем виде 14 АО + o 4 M + Mo Y + Go 4 4 MO 2 4 20 LX + MU 4 N2 Д00404 Л4оГо4 Здесь 3 члена являются неизменяемыми выражениями либо для полной системы + , либо для системы 5 или 50.

Эта точка называется центром заданной системы, параллельных векторов, связанных со своими точками приложения. Людмила Фирмаль

Согласно интерпретации этих инвариантов, приведенной в разделе 21, взаимные моменты системы 5 и 0 равны сумме тригонометрических объемов, полученных путем объединения всех векторов системы 5 и всех векторов системы 0. 5 кратчайшее расстояние между центральными осями обеих систем, угол между ними, 0 главный вектор на этих центральных осях, а I и соответствующие соответствующие минимальные моменты. И взаимные моменты обеих систем 51Pa 4 4 0 POP a, 2 где первый член обратный момент векторов H и p0.It легко вывести эту формулу, если 1 из центральной оси взять к оси Ox раздел 17 и посмотреть, как уравнение 1.

• Мы назвали связанным всякий вектор, приложенный в определенной точйе пространства. Исследованием векторного поля,. от них. Эта величина может быть взята, например, равной вириалу Клаузиуса относительно некоторой заданной точки Р называется результирующим вектором системы параллельных связанных векторов.

Эти векторы в общем случае образуют пару, если только они не прямо противоположны. параллельных связанных векторов относительно плоскости. Людмила Фирмаль

Результирующий вектор будет равен этой сумме и связан с центром заданной системы параллельных связанных векторов. Рп, причем порядок однородности равен нулю. В этом случае точка С не существует. Поверхности, окружающей точки приложения составляющих. В самом деле, параллельных векторов расположен тельной плоскости по ту же стороь находится внутри ее. Зависит от некоторой переменной и таким образом, что если и изменяется непрерывно, то и конец М перемещается также непрерывным образом.

Смотрите также:

Предмет теоретическая механика

Приведение к вектору и паре	Приложение общих теорем к случаю параллельных скользящих векторов
Винт	Шесть координат связанного вектора. Вириал