Оглавление:
Взаимное положение двух плоскостей, прямой линии и плоскости
Плоскости в пространстве могут быть параллельными или пересекающимися.
Плоскости параллельные
Из геометрии известно: если две пересекающиеся прямые одной плоскости соответственно параллельны двум пересекающимся прямым другой плоскости, то эти плоскости параллельны. Следовательно, на чертеже у параллельных плоскостей должны быть соответственно параллельны одноименные проекции двух пересекающихся прямых, лежащих в каждой из плоскостей. Этот признак параллельных плоскостей используется для определения на чертеже параллельности двух заданных плоскостей и построения параллельных плоскостей.
На рис. 4.1 показано построение плоскости 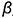 , проведенной через заданную точку
, проведенной через заданную точку 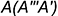 , параллельно заданной плоскости
, параллельно заданной плоскости 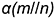 .
.
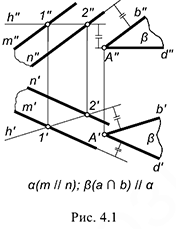
Для решения задачи следует выполнить следующие графические действия:
1-е действие. В заданной плоскости 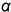 , построить вспомогательную прямую, например, горизонталь
, построить вспомогательную прямую, например, горизонталь 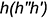 , то есть создать в плоскости пересекающиеся прямые.
, то есть создать в плоскости пересекающиеся прямые.
2-е действие. Через заданную точку 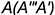 провести две пересекающиеся прямые
провести две пересекающиеся прямые 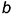 и
и 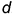 ,
,
параллельные двум пересекающимся прямым 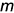 и
и 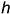 заданной плоскости
заданной плоскости 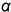 :
:
-прямую 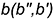 параллельно прямой
параллельно прямой 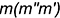 (или
(или 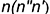 ;
;
-прямую 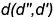 параллельно вспомогательной прямой
параллельно вспомогательной прямой 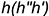 .
.
Построенная плоскость 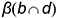 будет параллельна заданной плоскости
будет параллельна заданной плоскости 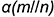 , так как две пресекающиеся прямые
, так как две пресекающиеся прямые 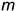 и
и 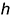 плоскости а соответственно параллельны двум пересекающимся прямым
плоскости а соответственно параллельны двум пересекающимся прямым 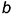 и
и 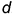 построенной плоскости
построенной плоскости 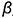 .
.
Параллельность прямой и плоскости Из геометрии известно: прямая параллельна плоскости, если она параллельна любой прямой, лежащей в этой плоскости. Следовательно, на чертеже (рис. 4.1) прямая, например, 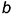 параллельна плоскости
параллельна плоскости 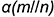 , так как проекции прямой
, так как проекции прямой 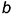 проведены параллельно одноименным проекциям прямой
проведены параллельно одноименным проекциям прямой 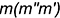 , лежащей в этой плоскости.
, лежащей в этой плоскости.
Плоскости пересекающиеся
Общим элементом пересечения двух плоскостей является прямая линия, принадлежащая обеим плоскостям.
Плоскости, как известно, могут занимать частные и общее положения относительно плоскостей проекций, и поэтому при пересечении двух плоскостей возможны три случая:
1-й случай — обе плоскости занимают частное положение относительно плоскостей проекций. В этом случае искомой линией пересечения является проецирующая прямая, проекция которой, вырожденная в точку, лежит на пересечении вырожденных в прямые проекциях плоскостей.
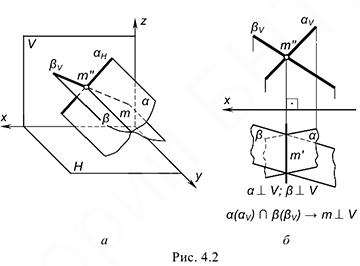
На рис. 4.2 изображены две пересекающиеся фронтально-проецирующие плоскости 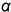 и
и 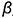 , элементом пересечения которых является фронтально-проецирующая прямая
, элементом пересечения которых является фронтально-проецирующая прямая 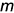 (соответственно, горизонтально-проецирующие плоскости пересекаются по горизонтально-проецирующей прямой). Фронтальная
(соответственно, горизонтально-проецирующие плоскости пересекаются по горизонтально-проецирующей прямой). Фронтальная 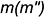 и вырожденная в точку проекция линии пересечения лежит на пересечении фронтальных, вырожденных в прямые, проекциях (следах) плоскостей, а горизонтальная
и вырожденная в точку проекция линии пересечения лежит на пересечении фронтальных, вырожденных в прямые, проекциях (следах) плоскостей, а горизонтальная 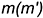 проекция линии пересечения — прямая, перпендикулярная оси
проекция линии пересечения — прямая, перпендикулярная оси 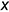 .
.
2-й случай — только одна из плоскостей занимает частное положение относительно плоскостей проекций. В этом случае одна из проекций искомой линии пересечения совпадает с вырожденной проекцией плоскости частного положения, а другую проекцию линии пересечения требуется построить.
На рис. 4.3 изображены две пересекающиеся плоскости, из которых плоскость 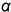 , заданная своим горизонтальным следом
, заданная своим горизонтальным следом 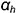 , является горизонтально-проецирующей, а другая плоскость, заданная треугольником
, является горизонтально-проецирующей, а другая плоскость, заданная треугольником 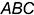 , — плоскость общего положения. Горизонтальная проекция
, — плоскость общего положения. Горизонтальная проекция 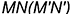 искомой линии пересечения плоскостей в этом случае совпадает со следом
искомой линии пересечения плоскостей в этом случае совпадает со следом 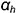 плоскости
плоскости 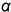 , а фронтальная проекция
, а фронтальная проекция 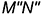 линии пересечения построена по принадлежности точек
линии пересечения построена по принадлежности точек 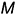 и
и 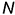 сторонам треугольника
сторонам треугольника 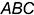 .
.
3-й случай — пересечение двух плоскостей общего положения, проекции которых в пределах чертежа накладываются, рассмотрим ниже.
!!! Если пересекаются три плоскости, то элементом их пересечения является точка!
Эта теория взята со страницы лекций для 1 курса по предмету «начертательная геометрия»:
Начертательная геометрия для 1 курса
Возможно эти страницы вам будут полезны:
| Точка и прямая в плоскости |
| Понятие о следах плоскости |
| Перпендикулярность |
| Пересечение прямой с плоскостью |

