Оглавление:



Взаимное пересечение поверхностей второго порядка. Особые случаи пересечения
- Пересечение вторичных поверхностей. Особый случай пересечения 1. Пересечение двух квадрических поверхностей является квартичной кривой 1. Другими словами, эта кривая пересекает плоскость в четырех точках (реальной и мнимой). В особых случаях пересечение квадратичных поверхностей может быть демпфировано, и особый интерес представляет разложение на пары квадратичных поверхностей.
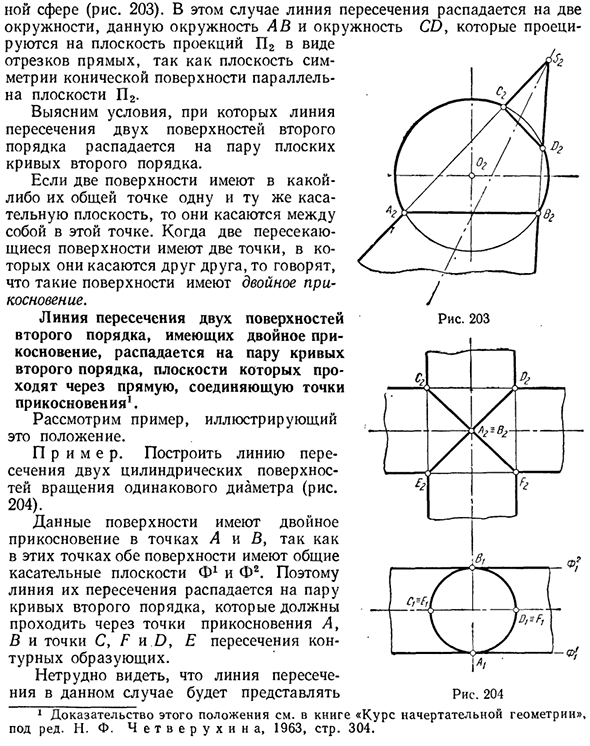
- В качестве примера рассмотрим пересечение сферы и вторичной конической поверхности. 1 Сфера (рисунок 203). В этом случае, поскольку плоскость симметрии конической поверхности параллельна плоскости P2, пересекающаяся линия делится на две окружности, заданную окружность AB и окружность CD, и проецируется в виде прямой линии на плоскость проекции P2.
Как известно, степень пересечения двух алгебраических поверхностей равна произведению порядка поверхностей. Людмила Фирмаль
Найти условия, при которых пересечение двух квадратичных поверхностей разбивается на пары квадратичных плоских кривых. Если две поверхности имеют одинаковую касательную плоскость в одной общей точке, они касаются друг друга в этой точке. Если две пересекающиеся поверхности имеют две точки, которые касаются друг друга, говорят, что такая поверхность имеет двойное касание.
Пересечение двух квадричных поверхностей двойным касанием разбивается на две пары кривых, и плоскость проходит через прямую линию, соединяющую точки касания. Рассмотрим пример, который иллюстрирует этот момент. Пример. Нарисуйте линию пересечения между двумя цилиндрическими вращающимися поверхностями одинакового диаметра (Рисунок 204).
В этих точках обе поверхности имеют общую касательную плоскость F1 и Ф2, поэтому они дважды касаются точек A и B. Следовательно, эти линии пересечения разбиваются на пары квадратичных кривых, которые должны проходить через точки касания A, B и точки C, F и D, E на пересечении генератора контура. Легко видеть, что линия пересечения в этом случае представляет собой диаграмму.
204 Рис. 203 1 См. Курс начертательной геометрии для доказательства этого утверждения. Под редакцией Н.Ф. Четверихии, 1963, с. 304. Это два идентичных эллипса, главные оси которых — CF и DE, а второстепенная ось — AB. Эти эллипсы проецируются на отрезки C2F2 и D2E2 на плоскости Y2 и на окружность, которая соответствует одному выступу на цилиндрической поверхности плоскости II. 2.
С помощью теоремы о двойном касании очень просто построить круглое сечение квадратичной поверхности, содержащей их. Для этого на этой поверхности нарисуйте сферу с двойным касанием. Эти пересечения затем разделяются на пары плоских кривых. Но кривая плоская. Если это находится на сфере, круге, это обнаружит круглое поперечное сечение вторичной поверхности.
Поэтому, чтобы создать круглое сечение вторичной поверхности, вы должны нарисовать сферу, которая дважды касается указанной поверхности, и ее пересечение обеспечивает пару круглых сечений этой поверхности. Давайте посмотрим на некоторые примеры. Пример I. Создайте круглое сечение эллиптического цилиндра (Рисунок 205).
Опишите сферу из любой точки O на оси цилиндра, касаясь и пересекая два генератора цилиндра. Контакты M и N являются точками контакта обеих поверхностей, поскольку они могут нарисовать общую касательную плоскость F1 и Ф2. Вот так. Поскольку на вторичной поверхности происходит двойное касание, линия пересечения разбивается на пару плоских кривых.
- В этом случае он делится на пару окружностей AB и CD в плоскости, спроецированной спереди. Две круглые секции полученного цилиндра включены в две серии круглых секций цилиндра, параллельных друг другу. Пример 2. Создание круглого сечения эллиптического конуса (рис. 206). Как и в предыдущем примере, напишите сферу с центром в точке O на оси конуса, чтобы добиться двойного касания с конусом.
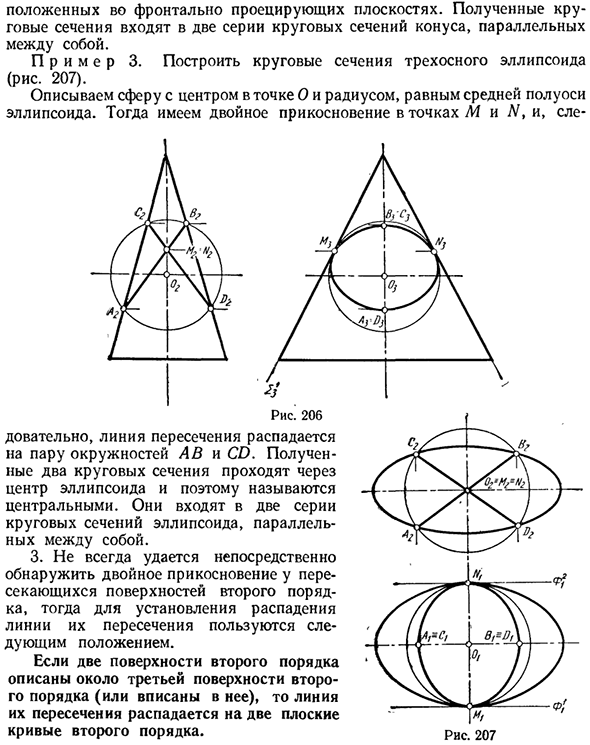
В точках M и N на обеих поверхностях имеются общие касательные плоскости 21 и 22. Далее линия пересечения делится на пары окружностей AB и CD. Он расположен на передней проекции плоскости. Получающиеся круглые секции включены в две серии круглых секций конуса, которые параллельны друг другу. Пример 3. Создание круглого сечения 3-осного эллипсоида (рис. 207).
Запишите радиус с центром в точке O и радиус, равный центральной оси эллипсоида. Людмила Фирмаль
Затем дважды коснитесь в точках M и N, затем Рис. 206 Линия пересечения разбита на пары окружностей AB и CD. Получающиеся два круглых сечения называются центром, потому что они проходят через центр эллипсоида. Они входят в две серии круглых сечений эллипсоидов, параллельных друг другу. 3.
Поскольку не всегда возможно обнаружить двойное касание непосредственно на второй пересекающейся поверхности, y Следующие местоположения используются, чтобы сформировать линию свертывания пересечения: Если две вторичные поверхности описаны (или вписаны) вблизи вторичной третьей поверхности, линия пересечения разделяется на две вторичные плоские кривые. Рис. 207
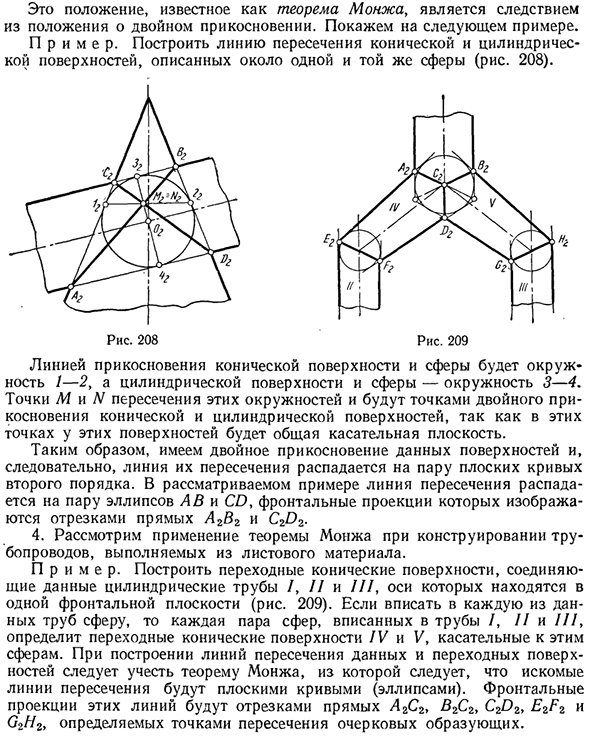
Эта позиция, известная как теорема Монжа, является результатом предложения двойного касания. Например: Пример. Нарисуйте линию пересечения между конической и цилиндрической поверхностями, нарисованными около одной сферы (Рисунок 208). Рис. 208 Рис. 209 Линия контакта между конической поверхностью и сферой представляет собой окружность / -2, а окружность между поверхностью цилиндра и сферой представляет собой окружность 3-4.
Точка пересечения этих окружностей M \ \ N является точкой двойного касания для конической и цилиндрической поверхностей. В этих отношениях эти грани имеют общую касательную плоскость. Следовательно, поскольку эти поверхности соприкасаются вдвойне, их линии пересечения разбиваются на пары квадратичных плоских кривых.
В этом примере линия пересечения разделена на эллиптическую пару AB и CD, а прямая проекция представлена отрезком прямых A2B2 и C2D2. 4. Рассмотрим применение теоремы Монжа при проектировании трубопроводов из листового материала. Пример. Создают переходную коническую поверхность, соединяющую эти цилиндрические трубы /, II, III. Эти оси находятся на одной и той же передней стороне (Рисунок 209).
Если сфера вписана в каждую из этих труб, каждая пара сфер, вписанная в трубу //, //, ///, определяет переходные конусы IV и V, соприкасающиеся с этими сферами. Теорема Монжа должна быть принята во внимание при построении пересечения данных и поверхности перехода. Из этой теоремы искомая линия пересечения представляет собой плоскую кривую (эллипс). Фронтальная проекция этих линий представляет собой отрезок линий ArC2B2C2y C2D2> E2F2 и G2H2y, определенных пересечением генераторов контура.
Смотрите также:
Начертательная геометрия 1 курс

