Оглавление:




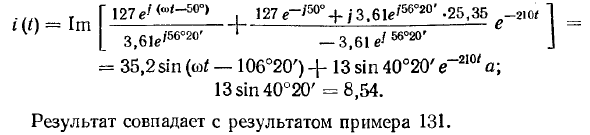

Вывод формулы разложения
Вывод формулы разложения. Предположим, вы представляете функцию времени, такую как изображение тока, в виде дроби. Чтобы получить ток как функцию времени i (/), сначала представьте простое дробное суммирование.
- Для этого замените x на p в формуле (10.58x): A» (0). M (p) full) ”1-yp ~ PkM ‘(Pk) P-Pk (10.60) Оригинал слева — это i (/). Оригинал справа — это оригинал термина ^ Принимает во внимание термин Ll.
Давайте перейдем от изображения к оригиналу. Людмила Фирмаль
Коэффициент суммы правой части термина A4 (0) PkM ‘(Pk) (10.60) является константой (не функцией p!), А константой Изображение само является константой, тогда рассмотрим, что правая функция p является лишь фактором — они соответствуют функции времени в форме ep k [справочное выражение (10.28) 1.
Следовательно, i (/) = + V_ (10.61) 44 (0) ^^ ркМ ‘(р „)’ Переход от изображения (функция p) к оригиналу (функция /) с использованием формулы разложения (10.61) На основании.
- Изображения были представлены в виде констант — и есть более простые дроби вида M (0) «<» N (Pk) p — и эти дробные элементы PkM ‘(Pk) P-Pk являются экспоненциальными Функция — er l rILr) Этот термин является компонентом тока или напряжения, которое ищется для постоянной e. е для д.с. констант.
Для цепей d.s = 0. Количество M (0) членов — ** равно числу корней выражения M (p) -0. Коэффициент — сравнивает с интегральной константой дифференциального уравнения (или уравнения)
в цепочке классических методов расчета. Людмила Фирмаль
Важно отметить следующее в уравнении (10.61): 1. Формула разложения применяется к начальным условиям и форме фактически генерируемого напряжения, действующего на цепь. 2. Если начальное условие ненулевое, вы найдете представление о том, что в состав N (p) входит «внутренний» e d.s 3.
Если в уравнении M (p) = 0 имеется корень комплексного сопряжения, то соответствующий член в уравнении (10.61) также является комплексным сопряженным, и получается весь член. 4. Действуя по схеме e. ds sine sine (<о / 4 ”Ф) 1 и изображение е. принимает вид ds Em —-, p- / co., где комплексная амплитуда равна Em-Åе ^.
При переходе от комплексного числа к мгновенному значению с помощью формулы разложения необходимо взять коэффициент с / (принять мнимую часть) *. Согласно этому «внутреннему» ds, ненулевое начальное условие цепочки синусоидальной волны e Отображается в правой части формулы разборки.
Вам нужно умножить d.s. на коэффициент /. Умножает внутренний e. d.s Требуется в j, потому что внутренние emfs существуют только в этом случае. Это учитывается при получении мнимой части с правой стороны формулы разложения. В цепи константы е. d.s Внутренние e. Нет необходимости умножать d.s j. 5.
Если напряжение, действующее на цепь, представляет собой синусоидальную волну, обязательный компонент решения включается в число членов ^ и определяется корнем p =]. В принципе, вычисление обязательного компонента как члена этой суммы, соответствующей корню p-jto сложной схемы, немного сложнее, чем вычисление напрямую с использованием символических методов.
Следовательно, для сложных цепей переменного тока рекомендуется вычислять обязательный компонент символическим методом, а не как компонент суммы уравнения (10.61), соответствующий корню p = jo.
Конечно, вы можете использовать уравнения, аналогичные уравнению (10.61), для определения не только тока и напряжения, но и других функций времени (зарядка конденсатора, скорость механической системы и т. Д.). Давайте рассмотрим два примера применения формул разложения.
Пример 142. Используя уравнение разложения 311 для определения тока (/) в схеме на рисунке, сравните его с результатом классического решения (см. Пример 129 на стр. 381): Å-150 ×; Rt -R’t-Ra-50 Ом, С = 100 мкФ. Решения. Создайте уравнение для текущего изображения в соответствии с законом Кирхгофа **.
Схема считает, что ненулевыми начальными условиями являются: A (p) 1 1 + сc (0) + = £; L (P) + f (P) b = E; lt (P) -L (P) ~ / s (P) = 0, где qs ( 0) = 50 означает «внутри» e. д.с., для накопления энергии в электрическом поле конденсатора до начала переходного процесса. *
Для данного e мнимая часть используется вместо действительной части формулы разложения. d.s Et sin (cof4-ф) — сложная мнимая часть Å ^ ‘4 (см. стр. 115). ** Создание схемных уравнений после переключения.
Из трех уравнений f (p): y (p \ = 1 £ -cc (0)] Я Cp + E = (p) 1 Вт RiR3Cp + Rl + R3 M (p) ‘*} + *? = -400 секунд ~ ‘-, Корень уравнения R & C M (p) = 0 есть p = LC0) = E = 150. m (0) = /? ! + /? s = 100; M ‘(pt) =?, С3C = 50 • 50 • 100 • 10 — == 0,25; L / (p,) = (150-50). 50,100 (- 400). От 10 до «+150 = -50; 150, (-50) e-» w <100 * (~ 400) «0,25 1,5 + 0,5e’wa, что соответствует результату примера 129.
Пример 143. Найдите i (t) в схеме на рисунке: 315 Классический метод применения формулы разложения и сравнения результата с результатом решения той же задачи (см. Пример 131 на стр. 384)
Решение. Изображение ds 127 sin (314 / –50 °) для e равно: Е (р) = Р — ДО, где Ет = 127р- / 5 ° c, начальное условие этой схемы не равно нулю: 7 (P) (Kr + pL) = E (p) + Lpi (0), e для действия в схеме, ds — синусоида, а ее изображение — Åт —-—, где Åт — комплексная амплитуда P-ju да В будущем коэффициент мнимой части должен быть получен из правой части формулы разложения (см. §301 §4) и умножен на «внутреннюю» e. d.s / Lpi (O).
После небольшого преобразования находим f (p): y (p \ = Etp + 1 LPi (p) (pk) = N (p). КK (p) = р + + jLpi (0) (p-jo ); M (p) = (pj <£>) (Kr + pL). Уравнение M (p) = 0 имеет два корня: Pi = sec-1 и p2 — = -210 sec «1 ‘N (0) = 0, поэтому первый член формулы (10.61) отбрасывается: L4’ (p) — / 2 + pL- [~ L (p- / co); M ‘(P,) = 24-3 / = 3,61 e’56 * 2®1; M ‘(pg) = -3,61 e756 «20’;
Смотрите также:
| Формула разложения. | Переходная проводимость. |
| Условия на границе раздела проводящего тела и диэлектрика. | Понятие о переходной функции по напряжению. |

