Вывод формулы Грина

Оглавление:

Вывод формулы Грина

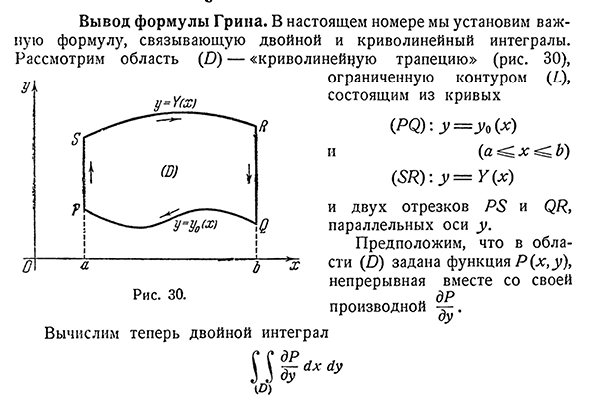
Вывод формулы Грина. В этом выпуске мы установим важную формулу, соединяющую двойной Интеграл с Интегралом кривой. Область (D) — «кривая трапеция» (рис. 30), ограниченный контуром (L), состоящим из кривой (P (2): y=y (x) (a x b) (5/? ): ^=Y (x) два сегмента

и<2/?параллельно оси Y. Предположим, что в области (I) задана функция P (x, y), а ее производная K непрерывна С d P Теперь вычислим двойной Интеграл I3461§3. Формула Грина 261 ? (икс ) Uounit () По формуле (6) n°344; получаем 5%<1У. (^)

Тогда (X) Внутренний Интеграл здесь может быть легко вычислен с помощью Людмила Фирмаль

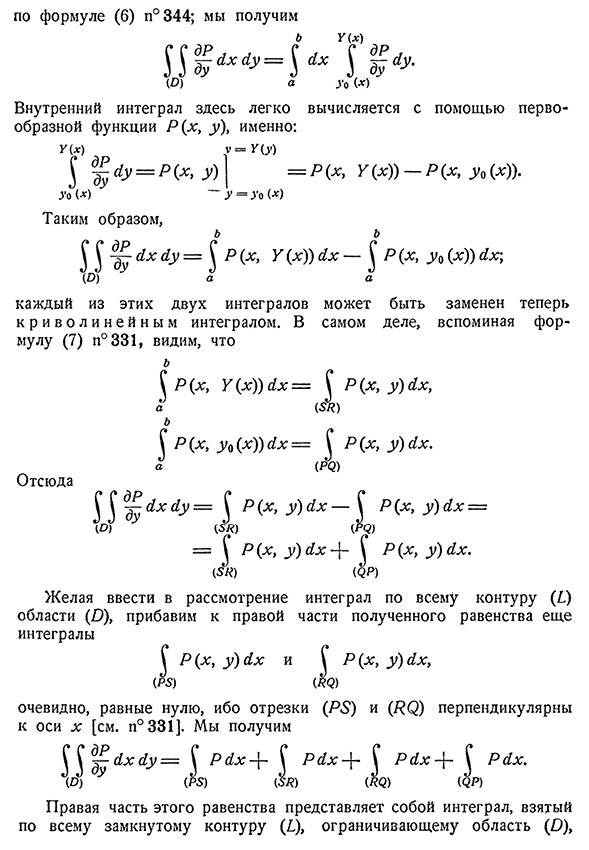
примитивной функции P (x, y: Г (х)Г=К(т ) $д — ^(1У=Р{х,г)|=р(х,г(х г)-р(х, г,(х))). Тогда{X)~~y=тогда(X) Таким образом, b§§^~L hs1u=R(x, Y (x}) y x — §R(x, y0 (x)) s1x; Мы можем заменить его на скорость восстановления реальности.- (О) » в Каждый из этих двух интегралов является интегралом. В Mulu (7) N°331, b(R (x, y (x)) yx=C R(x, y) yx,a(I?Б ) I R(X, D / O (X)) (/X=I R( X, y) y x. но Итак^^y x y — §R(x, y) y x-Y R (x, y) LX — (О) (5

шт) (д) ) =Р(х,.г)г Х4~Р (х, г) УГ. (5P) (ФР) Мы надеемся добавить больше интегралов в правую часть полученного уравнения, принимая во внимание интегралы для всего контура (I) области (O) Р(х, г) л X я§Р(х, у) (1х, (Р5)(Я<2) Явно равный нулю, отрезок(P5) и (/?(?) см. перпендикуляр к оси x[n°331]. Получаем S/^y x y=§R A x±§R s1x — ^Y RL x+RLX. (Я)у(р$)($я) (д) (^р) Правой частью этого равенства является Интеграл, который окружает весь замкнутый контур (L),

окружающий границу области(/?), 262ЧАП. XXI. двойной Интеграл[346 Однако о т р и К а т е л ь н о м направлении. В соответствии с установленным нами соглашением о обозначении интеграла кривой в замкнутом контуре[n°332], мы можем переписать полученное уравнение следующим образом: (1)это уравнение выведено из предположения о правильном направлении оси, но, как можно легко видеть, предполагается, что это левое направление (только положительное направление оси). Ранее мы предполагали, что фигура

(О) является»изогнутой трапецией»типа, показанного на рисунке. 30, и справедливость Формулы (1) доказана только для таких областей. На практике это относится и к областям, ограниченным контурами более сложных форм. Достаточно предположить, что прямая фигура (о), параллельная оси Y, может быть разложена на ряд вышеупомянутых «трапеций кривой» (например, см. рисунок). 26). Запишите каждую из формул в виде(1) отдельно и добавьте все такие уравнения. Левая сторона приобретает двойной Интеграл, распространяющийся на всю область(/9), а на правой стороне-сумму интегралов, которые принимают все частичные контуры.

Однако, поскольку Интеграл для каждого из вспомогательных сегментов Людмила Фирмаль

равен нулю, эти интегралы сводятся к интегралу по общему контуру (L). Поэтому и в этом случае устанавливается Формула(1). Аналогично выражение^y x y y=Y in (x, y)<1U(2) (O В предположении, что функция<2 непрерывна в области (O) вместе с ее частичным дифференцированием^ -. При этом сначала для области (7? Изогнутая трапеция (по форме, как показано на рисунке). 31. Он заключен в кривую (P8′)\x=x^y) и (C^y^s G) (OK) -, x=X (y) 347]§3. Формула Грина 263 И два сегмента (RO) и (5/?), параллельно оси X. Эта формула обобщается в случае области, которая, как упоминалось выше, разложена линией, параллельной оси x, в трапецию такого рода

конечного числа кривых. Наконец, если область (O) удовлетворяет условиям обоих случаев одновременно, то есть она разлагается на трапецию конечного числа первого типа и (независимо) делится на конечное число второго типа. Ноль.-) (О) (3) Это формула Грина). Z-это eqanie. Можно привести условия, при которых Формула (3) действительна в более обозримой форме. То есть, по формуле Грина, любые подопечные имеют кусочно-гладкий контур. Мы этого не докажем.

Приведение двойного интеграла к повторному в случае криволинейной области.	Выражение площади с помощью криволинейных интегралов
Механические приложения	Интеграл по простому замкнутому контуру