Оглавление:



Вывод формул для напряжений на наклонных площадках при плоском напряженном состоянии
- Вывод формулы стресса Плоский наклонный участок Стрессовое состояние Для плоских задач рассмотрим только одно семейство наклонных платформ, то есть платформ, которые перпендикулярны
поверхности нагруженного параллельного шестигранника. Мы разрезаем основной параллелепипед, как показано на рисунке.
Выберите базовую треугольную призму из наклонного сечения, Людмила Фирмаль
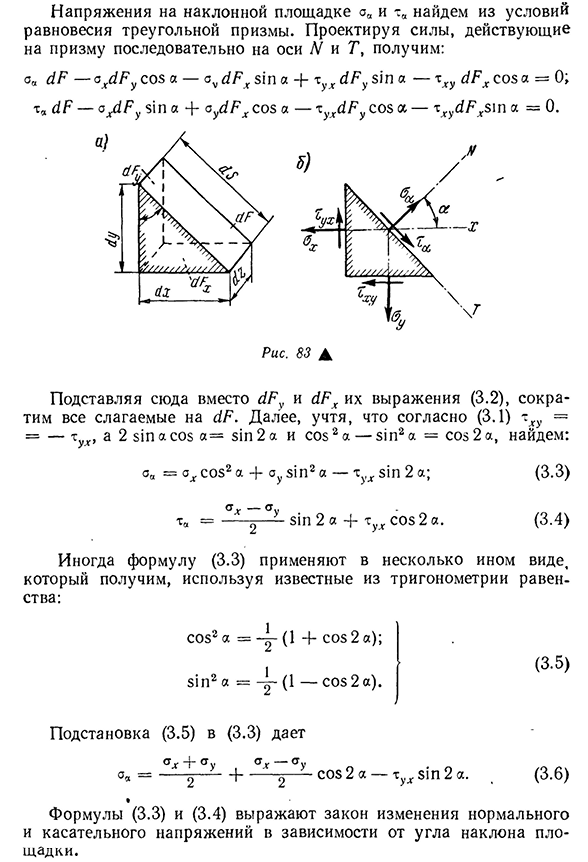
перпендикулярного плоскости 81 Сюй (рис. 83, а). Наклон участка с требуемым напряжением будет определять угол a, который формирует внешнюю нормаль к этому участку с осью x (рис. 83, б). Считая угол а, против часовой стрелки мы думаем положительно. С
рисунка. 83, и это будет dFy-dzdy = dF cos a, dFx = dzdx == dF sin a. (3.2) * Более общая формулировка этого закона описана в §31. Напряжение 88 наклонных платформ AA и TA определяется по состоянию равновесия треугольной призмы. Когда сила, действующая на призму,
- проецируется последовательно на оси n и ось Т, AA dF- ° xdFy cos a-sv dFx sin a4 — xyx dFy sin a — xxy dFx cos a = 0; xa dF- ° xdFy sin a4 -aydFx a— ^ yxdFy cos ar ^^ sin a = 0 Здесь мы заменяем это уравнение (3.2) вместо dFy и dFx, сводя все члены к dF. Кроме того, согласно (3.1) XH = -XH и 2sin a cos a = sin2a и cos2a-sin2a = cos2a, aa = axe cos2a4 * Oy sin2a-x sin2a; xa ——? —- Грех 2a4-Cos 2a. (3.3) (3-4) Иногда уравнение (3.3) используется в несколько ином виде, полученном с использованием
известной эквивалентности тригонометрии: (3.5) Подставляя (3.5) в (3.3), а х4-стю а х стю п. п / о р. Ох … = —- 2 —— 1 —— 2 —- COS2a-XH Sin2a. (3.6) Уравнения (3.3) и (3.4) — это угол наклона площадки В зависимости от этого он представляет собой закон изменения нормального напряжения и касательного напряжения. Уравнения, полученные в главе 9, глава 9 для Ita при 89 простых напряжениях, являются частными случаями уравнений (3.3) и (3.4),
из которых AU = tug = 0 и ol, Получается с = O Для риса. Ссылочная позиция 84 Людмила Фирмаль
обозначает прямоугольный элемент, который является проекцией параллелепипеда, который отделен от тела в окрестности оси X от точки А под произвольным углом. Изучение взаимосвязи между нормальным напряжением и + 90 °. • Напряжение ОА определяется уравнением (3.6), а если вместо этого + 90 °, получено напряжение Гениева +90: х + стю ( + 90 ° = 2 + cos2 (+ 9 0 °) — грех 2 (4-90 °)), или Рис 84А х + стю ° a + 9 0o2 — g — cos2A + v sin2A. (3.7) Складывание (3.6) и (3.7), мы заключаем % ++ 90 ° — ° x + ° y = c o n st. (3. Восемь) Таким образом, в данной точке алгебраическая сумма нормальных напряжений для любых двух взаимно перпендикулярных узлов является постоянной величиной.
Смотрите также:
| Статически неопределимые конструкции | Зависимость между моментами инерции при повороте осей |
| Расчет гибких нитей | Главные оси инерции и главные моменты инерции. |

