Оглавление:



Высокоэластические деформации
- Высокая упругая деформация. Резина и резиноподобные материалы способны к очень большим упругим деформациям, которые во много раз превышают первоначальную длину. Такая деформация называется очень упругой (термины «упругость»и» эластичность »
являются синонимами). Природа упругости резины и других полимерных материалов принципиально отличается от природы упругости металлов. Молекулы высоких полимеров имеют вид цепочек, образованных повторением одних и тех же г
рупп атомов, Соединенных валентными связями. Каждая связь допускает Людмила Фирмаль
некоторую кинематическую свободу, так что цепеподобные молекулы связываются с запутыванием. Если на тело не действуют внешние силы, то среднее расстояние между концами молекул значительно меньше их длины в растянутом состоянии. Под действием силы молекулы вытягиваются, и после снятия нагрузки каждая из них
стремится вернуться в свое первоначальное состояние, что наиболее вероятно. Упругая энергия высокоэластичного тела может быть определена с большей или меньшей точностью, основываясь на теоретических соображениях молекулярной физики. Простейшее представление энергии в терминах кратности X,, x2 и X было бы
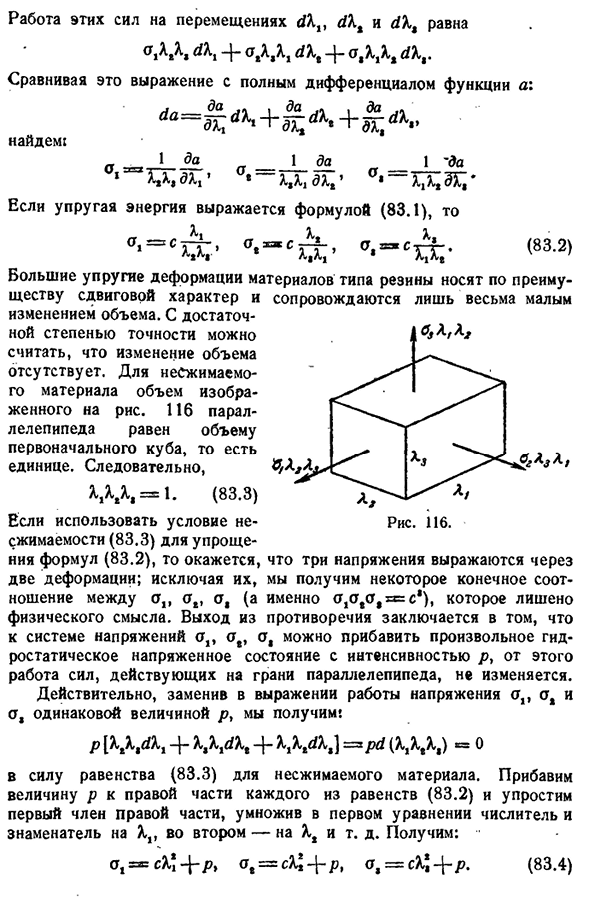
- (см.§ 81):): чтобы определить напряжение » a «=y C[X J -] — M4-M] » (83.1), мы говорим о конечной деформации, поэтому нам нужно исправить рассуждения предыдущего абзаца. Рассмотрим базовый объем, в котором ребро до преобразования было кубом, равным единице. После деформации OI разделяется на ребра X » x2 и X, (рис. И стал параллелепипедом). 116). Сила, действующая на его поверхность,
будет:_ _ _1 1 1 Да да>верфью h2x, ZX1 а»-x2×1z х,’<Т’ — x1×2 3 1/Если упругая энергия выражается в Формуле (83.1)、 (83.2) Большая упругая деформация материалов, таких как резина, в основном сопровождается сдвигом, только очень небольшими изменениями объема. С достаточной точностью можно предположить, что изменений в объеме нет. Для несжимаемых материалов объем показан на рисунке.
Параллелепипед 116 равен объему исходного куба, то есть, объем куба. Людмила Фирмаль
Следовательно, 4′ X, X, X, X,=1. (83.3) При использовании условия no-Fig. Чтобы упростить уравнение сжимаемости (83.3) (83.2), мы можем видеть, что три напряжения представлены двумя вариантами. Выход из противоречия состоит в том, что любое гидростатическое напряженное состояние с силой р может быть добавлено к системе напряжений О, О, О, О, из которой может быть приложена сила, действующая на плоскость параллелепипеда. Фактически, если мы заменим напряжениеa»-CX»+^ -. 2=2=0, x2=12.
Второе уравнение (83.5) дает: (83.5) В то же время Условие отсутствия давления принимает вид: 12X2=1. Введем формулу, найденную для P, в первое уравнение (83.5). Возьми: (83.6) Это уравнение кривой растяжимой резины, полученной стенкой. Она описывает деформацию резины в первом приближении. Чтобы получить более точный результат, вам нужно взять более сложное представление упругой энергии вместо (83.1).
Смотрите также:
| Конечная деформация | Упругое последействие |
| Нелинейно упругое тело | Некоторые свойства вязко-упругого тела |

