Оглавление:
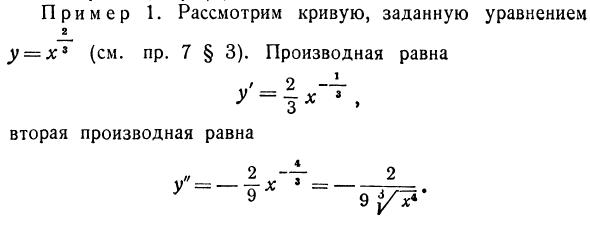



Выпуклость и вогнутость линии. Точка перегиба
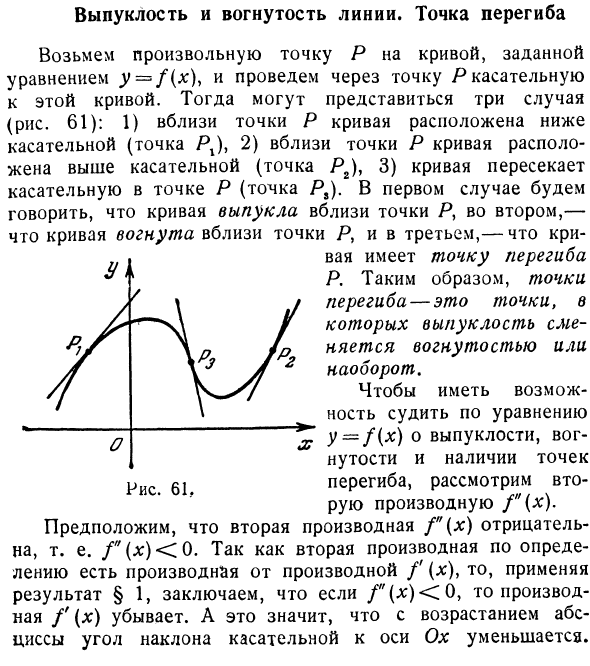
- Выпуклые и вогнутые линии. Точка перегиба Возьмите произвольную точку, возьмите кривую, заданную выражением y = f (x), и проведите касательную к этой кривой через точку через. Могут появиться три случая (рис. 61): 1) вблизи точки P, кривая находится ниже касательной вблизи точки P (точка PJ, 2), а кривая находится выше касательной (точка Я2), 3) Кривая пересекает касательную точки P (точка Я,). В первом случае кривая является выпуклой вблизи точки I, вторая кривая вогнута вблизи точки I, 3 Во второй кривой Существует точка перегиба P в качестве точки перегиба.
Чтобы можно было судить с выпуклостью y = f (x), Младенчество и наличие точек перегиба, Вывод производной f «(x). Предположим, что вторая производная f «(x) отрицательна, то есть f (x) <0. Поскольку вторая производная по определению является производной производной / ‘(x)>, результат § 1 Применяя f ‘(x) <. Если 0, производная f (x) уменьшается, что означает, что увеличение абсциссы уменьшает наклон касательной к оси Ox. /
Таким образом, точка перегиба — это точка, в которой выпуклая поверхность заменяется вогнутой поверхностью или наоборот. Людмила Фирмаль
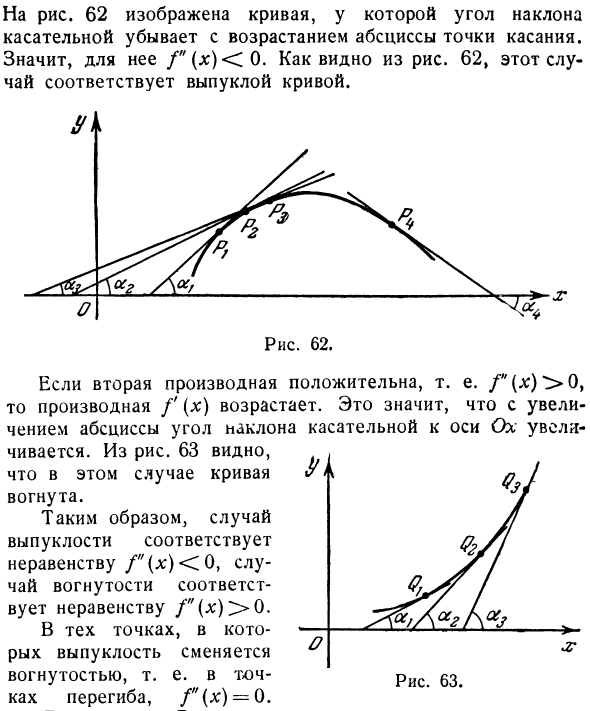
На фиг.62 показана кривая, в которой угол наклона касательной уменьшается по мере увеличения абсциссы точки контакта. Так что для этого / «(*) <0. Как видно из рисунка 62, этот случай соответствует выпуклой кривой. Если вторая производная положительна, то есть f (x) m> 09, производная / ‘(x) увеличивается. Это означает, что увеличение абсциссы увеличивает угол наклона касательной к оси Ox. Рисунок 63 показывает, что в этом случае кривая является вогнутой.
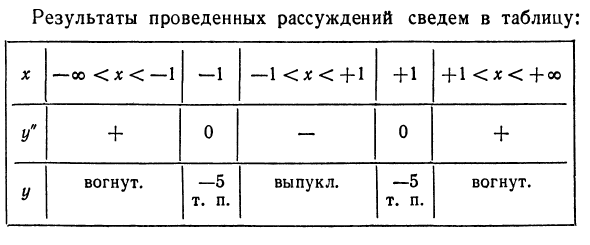
Следовательно, выпуклый случай соответствует неравенству f «(x) <0, а вогнутый случай соответствует неравенству /» (x)> 0. Точка, в которой выпуклая поверхность заменяет вогнутую поверхность, то есть Рефракционный излом, f (x) = 0. Пример 1. Рассмотрим кривую, заданную уравнением 2 у-х3 (пр. см. 7 § 3). Производная Вторые производные равны Поскольку вторая производная всегда отрицательна, кривая является выпуклой, и для Λ: == 0 производной не существует, поэтому график имеет вид, показанный на рисунке. 58. Значение независимой переменной с нулевой или без второй производной называется критическим значением второй производной.
- Вторая производная может изменить знак, только если она проходит критическое значение (см. § 1). Следовательно, точка перегиба является только критическим значением независимой переменной (см. Условия, необходимые для существования экстремальных значений). Изучение выпуклых и вогнутых кривых выполняется по плану, аналогичному плану экстремальных исследований.
Вот пример того, как это делается. Пример 2. Сначала найдите первую производную () функции: y’z = z4x * –12l: затем вторая производная: y «= \ 2x * -12 = 12 (n: 2-1). Найти критическое значение второй производной. Найдите важное значение из уравнения, потому что оно существует везде 12 (jc2-1) = 0, 1 = 0, xx = -1, lx, = +1
Изучите выпуклую и вогнутую поверхности кривой, заданной уравнением у = х * —6х2. () Людмила Фирмаль
Были найдены два важных значения. Эти значения нарушают ось l. 1) —oo <l2 <—1, 2) —1 <* <+1, 3) +1 В первом разделе вторая производная Есть второй знак плюс и третий знак плюс. Следовательно, при прохождении через x = -1 вторая производная меняет знак плюс на минус. То есть х -1 имеет точку перегиба.
После прохождения x = -j- \ вторая производная меняет знак минус на положительный. Это означает, что есть также точки перегиба.Результаты обсуждения сведены в таблицу. X-oo <* <-1 -1 -1 <x <+1 +1 + 1 <X <+00 Y «+ 0-0 + Есть вогнутая поверхность. —5 т. Выпуклый. -5 т Вогнутая поверхность.
Смотрите также:
| Исследование функций на возрастание и убывание | Общий план исследования функций и построения графиков |
| Максимальные и минимальные значения функции | Связь между графиком функции и графиком ее производной |

