Оглавление:
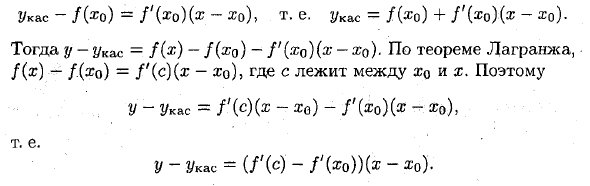


Выпуклость графика функции, точки перегиба
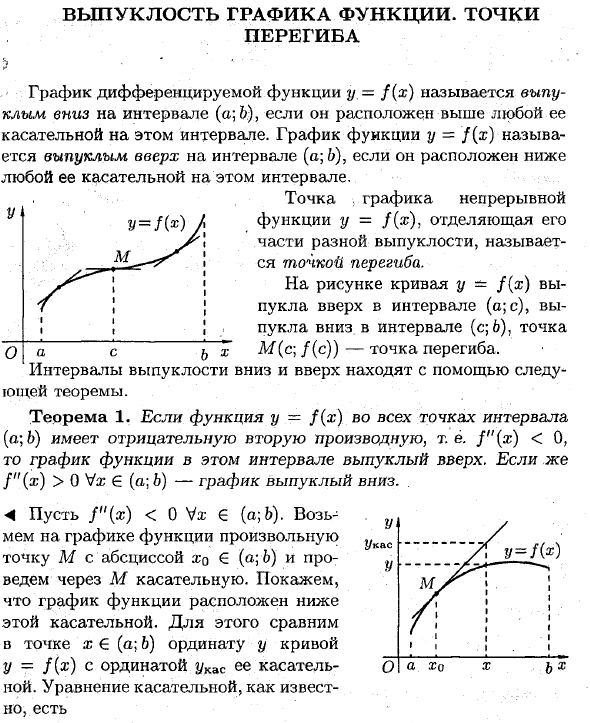
- Выпуклая функция графика, баллы сгибание в Y = 1 (х) > • Если график дифференцируемой функции y = f (x) называется выпуклым вниз в интервале (a; 6) и находится выше любой касательной в этом интервале. График функции y = f (x) называется вверх выпуклым в интервале (a; b) и лежит ниже любой касательной в этом интервале. Точка> на графике непрерывной функции y = f (x) разделяет различные выпуклые части и называется точкой перегиба.
На рисунке кривая y = f (x) выпукла вверх в интервале (a; c), выпукла вниз в интервале (c; 6), а точка M (c; f (c)) является точкой перегиба. х о Туз я) Расстояние выше и ниже выпуклой поверхности можно найти с помощью следующей теоремы. Теорема 1. Если f» (x)> 0 \ / x € (a; b), график выпуклый вниз. , G y = нет <«Пусть f» (x) <0 Va; e (a; b).
Если функция y = f (x) в каждой точке интервала, (a; b) имеет отрицательную вторую производную. f «{x) <0, график функции в этом интервале выпуклый вверх. Людмила Фирмаль
Возьмем произвольную точку M с абсциссой x $ € (o; b) в графе функций и проведем касательную через M. Для этого сравните ординату кривой y = f (x) в точке x € (a; b) с ординатой касательной кривой. Ykac-f (x °) = f ′ (x °) (x-Xo)> то есть 2 / ka = f (® °) + / ′ (® °) (®- * °). Далее y-2 / kas = f (x) -} {xq) -} ‘{xq) (x-xo). Согласно теореме Лагранжа, // (x) — /. (Xo) = f ‘(c) (x-xo), где c находится между xo и x. так Y-2 / kas = / Cs) (x— ‘(®o) (®-x0), Это Y-2 / kas = (/ ‘(c) — /’ (®o)) (x-
Разница f ‘(c) -f’ (xo) снова преобразуется по формуле Лагранжа. f, (c) -f ‘(x0) = f (c1) (c-x0), c1 находится между x0 и c. Таким образом, Y-Y * ac = f «(cj) (c-x0) (x-®o). Изучите это равенство. 1) Если x> x0, x-xo> 0, c-x0> 0 / «(Ci) <0. Следовательно, y-2 / kas <0, т.е. ®0GΓ 2 / <2 / cas1 2) Если x 0, то аналогично доказано, что график выпуклый вниз. ► Следующая теорема используется для нахождения точки перегиба функционального графа.
| Максимум и минимум функций | Асимптоты графика функции |
| Наибольшее и наименьшее значения функции на отрезке | Общая схема исследования функции и построения графика |
Примеры решения и задачи с методическими указаниями
| Решение задач | Лекции |
| Сборник и задачник | Учебник |
- Теорема 2. (Достаточное условие существования точки перегиба). Вторая производная} «Если знак изменяется при прохождении через точку x0, где {x) равен нулю или не существует, точка графа с абсциссой xq становится точкой перегиба. 0 для x> xo. Это означает, что левый график x = xo выпуклый вверх и выпуклый вниз вправо. Следовательно, точка (x0 ‘; / (® °)) на графике функций является точкой перегиба. Аналогично, если x 0 и x> xo и f «(x) <0, то точка (xo; / (xo)) будет преобразована в график функции y = / (x).
Пример: Изучите график функции точки выпуклости и точки перегиба y = xb-x H-5. Y ‘= 5×4-1, y «= 20×3. Вторая производная существует по оси значений. Если x = 0, y» = 0. y «> 0 для x> 0; y» <0 для x <0. Поэтому график функции y = xb-x + 5 интервала (-oo; 0) выпуклый вниз в интервале (0; oo) -. Точка (0; 5) — точка перегиба. ♦
Доказано, что песня точка., ‘► Людмила Фирмаль

