Оглавление:



Выпучивание упруго-пластического центрально сжатого стержня в условиях возрастающей нагрузки (понятие о теории ф. р. шенли)
- Эластичная пластиковая пряжка Уплотненные стержни в центре состояния Увеличение нагрузки(концепция 0) Ф. Р. Шэнли) В предыдущем пункте при теоретическом определении критической силы на стержень, сжатый за пределами пропорциональности, е [см. Формулу 1] уменьшил так называемый модуль упругости е [см. формулу(15.10)1 с конца прошлого века.С. Ясинский, T.It был
использован в таких работах, как карман и назывался теорией редуцированных модулей. Критическая сила, определяемая по формуле (15.10), называется приведенной модульной. Давайте представим его в РГ. Ф. Энгессер предложил определять критическую силу на Упругопластической стадии по уравнению Эйлера, а не по модулю упругости вместо величины касательного модуля E -=,
у вас есть 396). Эта сила называется P-модульной и обозначается Px. И так Людмила Фирмаль
оно и есть., TS2EG< / 7S2E t U R= — — — — — — * R=_ I — — — — — — (n02″ (^) 2 Ф. С. Со времени предложения Ясинского до недавнего времени теория редуцированного модуля считалась правильной, а теория касательного модуля считалась ошибочной, и в то время ее автор, однако, спустя полвека после работ Энгессера и Ясинского, появились новые идеи по этому вопросу, и правильность теории модуля при определенных условиях Ф в этом вопросе была доказана. 1946.R.It
впервые был высказан Шэнь-Ли, а позже обсужден в литературе многими авторами. Рассмотрим суть этих новых идей. В теории редукционного модуля существенным моментом является наличие разрядной зоны, которая образуется в момент выпуклости стержня (как указано в предыдущем пункте). Но глубина этой зоны в любом сечении стержня обычно зависит от двух факторов.- 471)в поперечном сечении при кривизне бесконечно малого стержня, от величины приращения силы yr с этим отклонением. В этом случае c1m способствует появлению зоны разряда, но увеличение силы<1P компенсирует это. Теория редукционных модулей соответствует
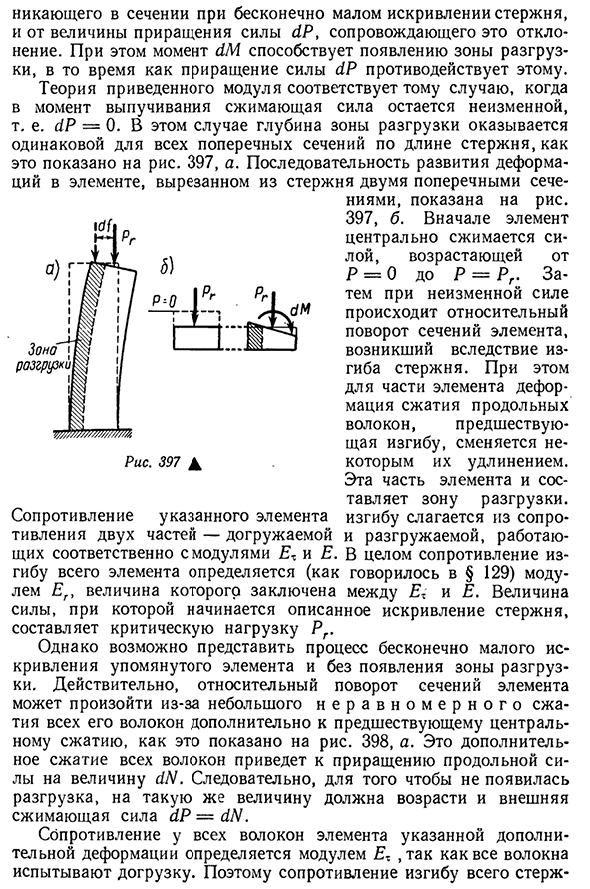
- случаю, когда сила сжатия не изменяется в момент потери устойчивости.Р-0 в этом случае глубина зоны разгрузки одинакова для всех поперечных сечений по длине стержня, как показано на рисунке. 397, а. последовательность развития деформации элементов была вырезана из стержня двумя поперечными сечениями- Рис 397А Как использовать 397, b. во-первых, элементы сжимаются к центру за счет увеличения сил от p=0 до P=RG. Затем с определенной силой происходит относительное вращение сечения элемента за счет изгиба стержня. В этом случае для некоторых элементов деформация сжатия продольных волокон, предшествующая изгибу, заменяется
некоторым растяжением. Эта часть элемента является зоной разгрузки. В общем случае определяется полное сопротивление изгибу элемента (как описано в§129) модулем EG, и его значение заключено между E? Величина силы, с которой начинается описываемая кривизна стержня, является критической нагрузкой RG. Однако можно представить себе процесс с бесконечно малой кривизной вышеперечисленных элементов и без появления Зоны разряда. На самом деле, помимо предшествующего Центрального сжатия, относительное вращение секций элементов может происходить за счет малого п е б н о м е р н о г о сжатия всех его волокон. 398, а. это дополнительное сжатие всех волокон приводит к увеличению продольных сил на величину no.
Поэтому, чтобы не казаться разгруженным, то же значение должно быть увеличено и внешнее усилие сжатия c1p-no. Сопротивление всех волокон Людмила Фирмаль
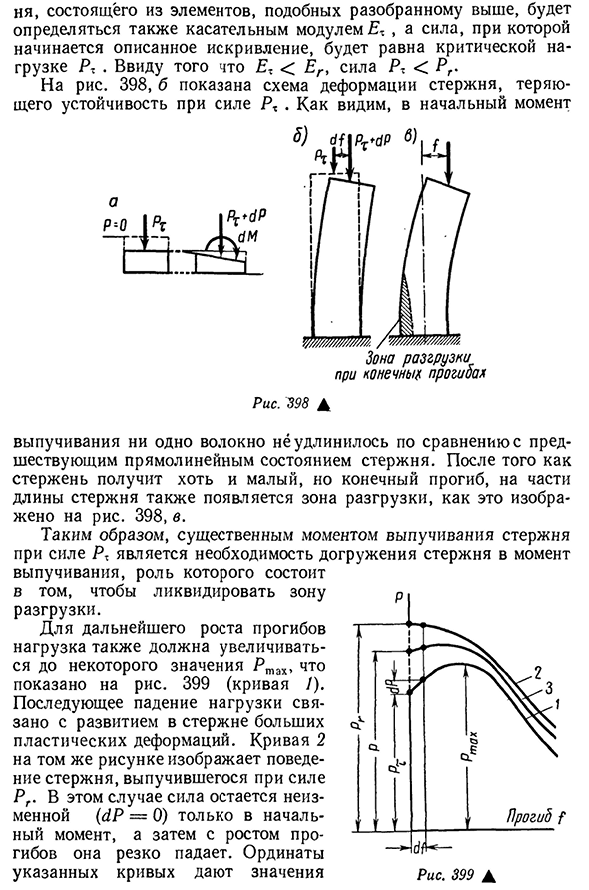
элементов указанной дополнительной деформации определяется коэффициентом Et, так как все волокна подвергаются дополнительным нагрузкам. Поэтому, гнуть сопротивление всего тела- 472 тело, состоящее из таких элементов, как описано выше, также определяется касательным модулем Eg, и сила, при которой начинается описанная кривизна, равна критической нагрузке RG. Ввиду того, что Е — <например, сила<РГ. Для риса. 398, б показана схема деформации стержня и потери его устойчивости с усилием РХ. Как видите, в первый момент После выпучивания волокна становятся не длиннее, чем в прямом состоянии перед стержнем. После получения окончательного прогиба, на части длины стержня также появится зона разгрузки, хотя стержень меньше, как показано на рисунке. 398 дюймов Поэтому существенный момент выпячивания стержня с усилием Р-это необходимость перезагрузки стержня в
момент выпячивания, роль которого заключается в устранении зоны разгрузки. Для дальнейшего роста прогиба нагрузка также должна увеличиться до некоторых значений RT a x, как показано на рисунке. 399 (кривая/). Последующее падение нагрузки связано с развитием большой пластической деформации в стержне. Кривая 2 того же рисунка показывает поведение стержня, накачанного силой RG. В этом случае сила остается неизменной только в первый момент(<1P=0), после чего она резко уменьшается с увеличением прогиба. Вертикальная ось этих кривых дает значение 473cil может
быть уравновешен стержнем с заданным отклонением. Например, если внешняя сила достигает величины Rtah (кривая/), то рост прогиба не может быть уменьшен, это приводит к дисбалансу и ускоренному процессу разрушения стержня. Для риса. 399 пунктирная линия на вертикальной оси Центрального сжатого стержня показывает область, демонстрирующую неустойчивость к изгибу в упругопластической стадии. При любом креплении разница между обеспечением линейного состояния сердечника в процессе увеличения определенной силы Р между РТ и РГ и последующим освобождением сердечника от этих креплений заключается в том, что в первый момент выпуклости возникает зона разгрузки, и чем больше R, тем ближе к РГ. Необходимо, чтобы при изгибе с усилием меньшим, чем RG, требовались некоторые специальные условия для
обеспечения требуемого закона изменения силы с увеличением прогиба, в первый момент искривления ко-стержня нагрузка, действующая на него, возрастает. Это случай характерной нагрузки как при работе конструктивных элементов, так и при испытании стержня на Центральное сжатие. Так, если центральный сжатый стержень испытывает действие нагрузки, то он имеет целый диапазон ее критических значений: Р<р р<р г. Относительная модульная сила RT может рассматриваться как наименьшая критическая сила в этом стержне. Поскольку разница между
значениями Px и RG фактического стержня обычно очень мала, очень трудно проверить на опыте, какая сила стержня потеряет устойчивость. Это, вероятно, означает, что приведенное выше представление об относительной модульной силе как о самой незначительной силе стержня в условиях возрастающей нагрузки долгое время остается незамеченным.
Смотрите также:

