Оглавление:





Вынужденные колебания в физике
- Принудительная вибрация. Учитывайте вибрацию системы Несколько переменных внешних полей работают. Такая вибрация Абзац перед так называемой свободной вибрацией. Поскольку ожидается, что колебание будет небольшим, Это означает, что внешнее поле достаточно слабое.
В противном случае это может привести к выбросу x. В этом случае вместе со своей потенциальной энергией (1/2) x2 система также имеет потенциальную энергию C / e (x, Ј) Связано с внешними полевыми действиями.
Поскольку первый член является функцией только времени Людмила Фирмаль
Расширение этого дополнительного члена на серии малых степеней х приводит к Ue (x, t) ъ Ue (0, t) + x Их ах , он может быть опущен в функции Лагранжа (как полная производная от t для других функций времени). Во втором слагаемом — dUe / dx, существует внешняя «сила», которая действует на систему равновесия и является заранее определенной функцией времени.
Представлено F (t). потенциально Термин –xF (t) появляется в энергии, поэтому функция Лагранжа Система L = r ^ — * — + xF (t). (22,1) Соответствующее уравнение движения tx + kx = F (t), или x + w2x = -F (t), (22,2) T Здесь частота si свободной вибрации была введена снова.
- Как известно, общее решение гетерогенного линейного дифференциального уравнения с постоянным коэффициентом получается как сумма двух уравнений. х = х0 + х \, где хо- Общие решения однородных уравнений, а x \ являются частными интегралами неоднородных уравнений.
В этом случае x0 — это свободная вибрация, которая обсуждалась в предыдущем разделе. Рассмотрим случаи, представляющие особый интерес Применяемая сила также является простой периодической функцией времени с определенной частотой y. F (t) = / cos (yt + (3). (22,3) Частный интеграл уравнения (22.2) имеет вид x \ = b cos (yt + + (3) Тот же периодический фактор.
Любая константа определяется из начальных условий Людмила Фирмаль
Подставляя в уравнение: b = // [ha (cu2-y2)]; Добавление решения к однородному уравнению дает общий интеграл в виде x = a cos (cut + oc) +. / -cos (ут + (3). (22,4) т (си2-й 2) . Поэтому при регулярных принудительных действиях Система сил движется, что представляет собой комбинацию двух колебаний, собственной частоты си-системы и частоты движущей силы у.
Решение (22.4) не применяется в случае так называемой рез nanza. Когда частота движущей силы соответствует собственной частоте системы. Чтобы найти общее решение уравнения движения в этом случае, перепишите уравнение (22.4) как Соответствующая переопределение констант в виде x = a cos (cut + oc) H ———— ^ t [cos (yt + 6) -cos (cut + 6) 1. v 7 m (a) 2-y 2) 1 v 7 v / J Для y-y cu второй член дает неопределенность вида 0/0.
При открытии в соответствии с правилами Rittal, x = a cos (cut + oc) + sin (cut + (3). (22,5) Таким образом, в случае резонанса амплитуда вибрации линейно увеличивается со временем (до тех пор, пока вибрация не прекратится) И вся представленная теория уже не применима).
Также проверьте, как маленькие вибрации выглядят в непосредственной близости Если Nanza, y = si + e, где небольшое количество. воображать Общее решение в интегрированном виде x = Aeia) t + Be «w + Ј) * = (A + Beizt) eia) t. (22,6) Поскольку значение A + Beizt почти не меняется в течение периода Коэффициент эр * 2р / с, затем движение близко к резонансу Это считается небольшим изменением, но амплитуда является переменной х).
Если последний представлен C, C = \ A + Веш . Выражая Al B в форме эго и lef ^ соответственно: C2- ах? — \ — b2 — \ — 2a3cos (st | — (3-a). (22,7) Таким образом, амплитуда периодически изменяется с частотой е и изменяется между двумя пределами \ a-b \ ^ C ^ a + b. Это явление называется нападением.
Интегрирование уравнения движения (22.2) Общий вид произвольной движущей силы F (t). Это легко сделать, переписав следующее: ^ — {x + icox) -icvix + icox) = -F (t) дтм м или §- «и * = я м (22,8) Где вводятся комплексные числа Ј, = x + iwx. (22,9) Уравнение (22.8) является первым, а не вторым порядком. Нет права Часть его решения Ј, = Aeia) постоянная A t.
Как правило, мы ищем решения неоднородных уравнений вида Ј, = A (t) eta) t и функция A (t), уравнение Alt) = — m F (t) e˜iwt. При интегрировании вы получите решение уравнения (22.8) в виде: Здесь константы интегрирования Ј и о выбираются для представления значения Ј в момент времени t = 0. Это желательное общее решение. Функция x (t) задается мнимой частью (22.10) выражения (деленной на si) d).
Энергия системы вынужденной вибрации Конечно, не сохраняется. Система получает энергию из внешних источников. Определяет общую энергию, доставляемую в систему за весь период мощности (от -os до + os).
Предположим, что начальная энергия равна нулю. Согласно уравнению (22.10) (нижний предел интегрирования, не ноль —os Ј, (-oc) = 0), для t oc С другой стороны, энергия самой системы определяется Замените здесь на | Ј, (os) | 2 и получите желаемую передачу энергии в форме, определяемой квадратным коэффициентом фурье-компонента силы. F (t) с частотой, равной собственной частоте системы.
В частности, внешняя сила Короткий период (маленький по сравнению с 1 / си), e ~ ia) t «1. можно разместить. о (22.11) (22.12) Этот результат заранее ясен: это факт Вместо кратковременной силы, дающей системе импульс f F dt, В это время может возникнуть значительное смещение.
Задание 1. Определить вынужденную вибрацию системы под действием силы F (t), в первый момент t = 0, и система неподвижна в одинаковом положении Вес (х = 0, х = 0), если: а) F = const = F0 Ответ: x = —— (1-cos (Jot): Шея 2 Смещение положения равновесия, где возникает вибрация.
б) F = при. Ответ: x = —— (разрезать-отрубить). tshl Ti-OCT 3 / _ _ a (__ ,, a м (куб. г) F = враг, потому что (31. Ответ: в) F = F- Ответ: x = —-— —-— (e-cos cut + -sin cot). м (куб2 + 2) в куб / F0 m [(cu2 + a 2- (32) 2 + 4a2132] — (Cu -b oc | — (3) sin cut + e [(^ oc- (3) cos (31-2oc | 3 sin (31]) (В решении удобно описать силу в сложной форме F = ^ o ^ _x + r ^^). 2.
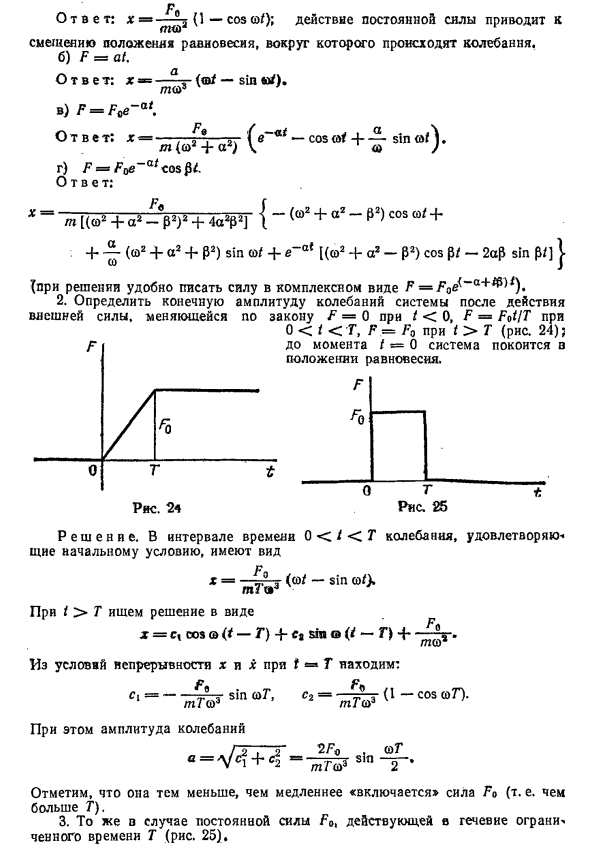
Я изменяю, чтобы определить конечную амплитуду вибрации системы после воздействия внешней силы t = 0, F = 0, F: F = Fot / T 0 T Fq (рис. 24); t = 0, система находится в равновесии. / | Я ^ 7701 Решения. Для временных интервалов 0 T, ищите решение в следующем формате: тр X = d cos [cu (t-T) 1 + C2 sin [cu (t-T) 1 + -> T. GT1 шея 2 Из t = T условия непрерывности x и x, ci = —— sin wT, C2 = — „(1-coswТ). tptsh3 «tptsh3 v» В этом случае амплитуда колебаний а =
Обратите внимание, что чем меньше сила Фо «вкл», тем медленнее Большой Т). 2 | 2 2F0. квасить 4 = — ^ — О грехе Tpt Si3 2 3. То же самое применимо, когда постоянная сила Fo прикладывается в течение ограниченного времени T (Рис. 25).
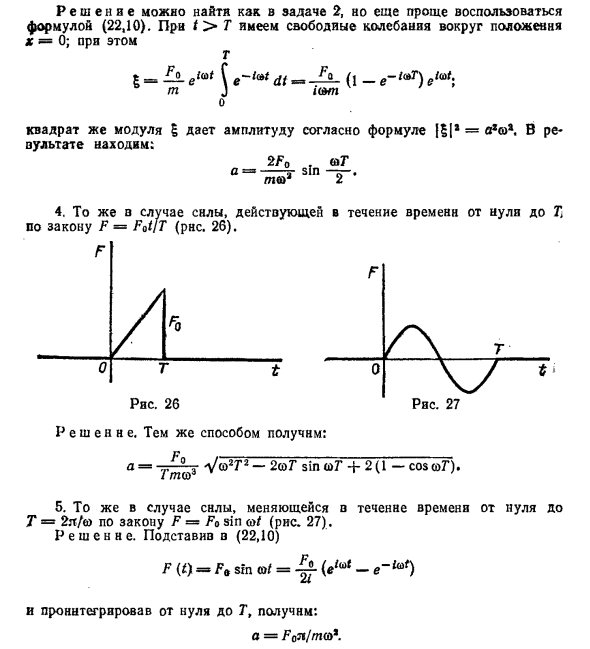
Решение можно найти как в задаче 2, но проще использовать формулу (22.10). t> T, есть свободная вибрация Положение х = 0; T Ј * F °, = —e м -i c v t j, F o-i w T \ i c v t е в = —— (1-е) е; ICVM Квадрат квадрата модуля дает амплитуду по формуле | Ј, | 2 = a2сi2. снова узнать Fo 0 т Рисунок 25 0 т Рисунок 26 2F0. заседать а = —— грех—. Шея 2 2 4.
То же относится и к силе, действующей во времени от нуля до Т Согласно закону F = Fot / T (рис. 26). Решения. Таким же образом a = „Fo, J w 2T2-2wT sm w T + 2 (1 − cos wT). Tmuo3 5. В случае изменения силы с нуля Т = 2п / ш — F = закон отсечения по закону (рис. 27). Решения. Назначить (22.10) Fit) = огранка греха = ^ (eiwt-e ~ iwt) 2 грамма Интегрирование от нуля до Т, Fqtc
Смотрите также:
| Рассеяние под малыми углами в физике | Колебания систем со многими степенями свободы |
| Свободные одномерные колебания | Колебания молекул в физике |
Если вам потребуется помощь по физике вы всегда можете написать мне в whatsapp.

