Оглавление:






Вынужденные колебания твердого тела с двумя степенями свободы с учетом гироскопических сил
- При составлении дифференциальных уравнений в этом случае можно использовать движение. Теорема об изменении главного момента импульса. Формула основных моментов импульса, определяемая уравнением 2, приведена в пункте 1 настоящего пункта Держите power. В отличие от ранее рассмотренных малых колебаний, момент возмущающей силы входит в основной момент внешней силы относительно неподвижной оси. Наиболее распространенной возмущающей силой, действующей на твердое тело, вращающееся вокруг оси, является сила, создаваемая дисбалансом в роторе.
При решении задачи определения вынужденного колебания твердого геля с 2 степенями свободы под действием силы гироскопа рекомендуется следующая последовательность действий 1 Выберите стационарную подвижную систему координат. 2 Составьте формулу главного момента импульса тела и главного момента внешней силы относительно неподвижных осей координат. 3 Использовать теорему об изменении основного момента импульса для нахождения дифференциального уравнения малых колебаний. 4 система дифференциальных уравнений, определяющая вынужденные колебания системы, ищущей конкретное решение. 5 резонансное явление возникает для определения критической угловой скорости Ротора.
В случае движения свободной материальной точки удобно пользо-ваться системой осей декартовых координат. Людмила Фирмаль
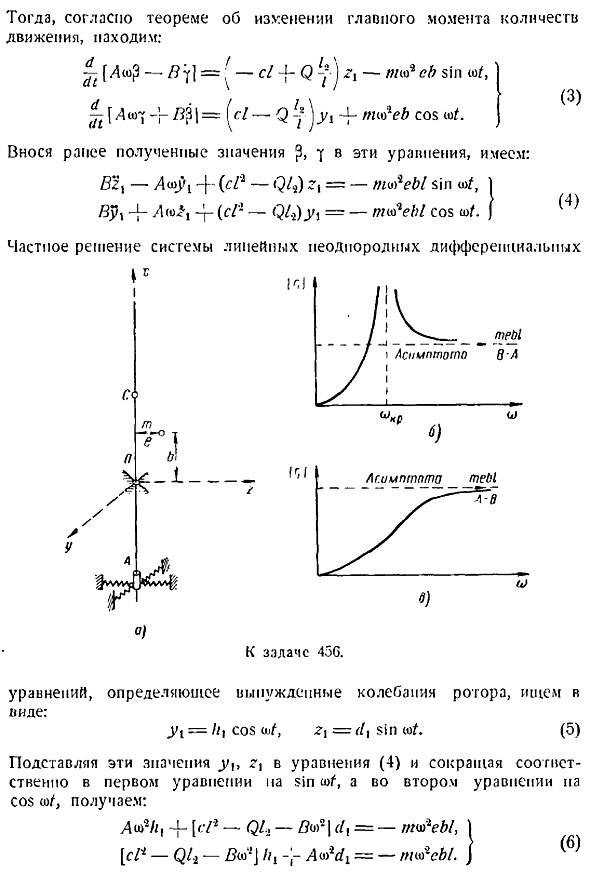
Найдите нужное переменное предельное значение, угол поворота ротора увеличится до неограниченного количества оборотов. Мы покажем, как вынужденная вибрация Ротора, вызванная врожденным дисбалансом, изучается в следующих примерах Проблема 456. Определить вынужденное колебание шпинделя при условии задачи 454, если он находится на высоте b над неподвижной точкой o рисунок А и на расстоянии е от геометрической оси k Ротор имеет малую массу, м, но малую массу d, поэтому игнорируют влияние изменения центра тяжести ротора и изменения момента инерции. Решение С и Е. Создайте дифференциальные уравнения для движения ротора, используя теорему об изменении основного импульса.
Момент на неподвижной оси равен Реакция нижней упругой опоры, силы тяжести и силы Р, реакция удержания массы Ротора связью. Сила p равна А м е. 1 ОА имеет ось, параллельную oy, и лежит в плоскости, параллельной созданию угла через точку, в которой находится масса m. Момент этой силы относительно неподвижной оси г Вы будете Т Р — м я е 6 2 тогда, согласно теореме об изменении главного момента импульса — ДНР — С1 2 г 2, -м л КБ 81n о 1 7 3 А 07 б — с — ЦУ М 4 Пич Е потому, что о. Вы уже приобрели эти формулы Если ввести значение 7, оно будет выглядеть следующим образом В2 — Ди 4 4 с — 24 i — m n ezt w, 1 Вух 4 Лго. 214 — 24 1 -m e const.
Конкретное решение для линейной неоднородной дифференциальной системы Голы 456 Уравнения, определяющие вынужденные колебания Ротора, представлены в следующем виде У1, что 3, Р4 s1n о. 5 Подставляя эти значения Формулы 4 для, уравнения и що соответственно в первое уравнение що и убывая в соз во 2-е уравнение соответственно, мы видим Ди 4- — 24- О 2 г, — tygey, с 2 — 24-Б Л — П a0a4 -м ЦН. 6 это решение было получено без учета сопротивления, которое препятствует вращению Ротора. Vibrating. No независимо от того, как мало сопротивление, это приводит к быстрому демпфированию свободной вибрации Он определяется в первых 2 терминах в правой части уравнения 10.
- Поэтому при исследовании вибрации, вызванной дисбалансом ротора в установившемся состоянии. Первые 2 члена справа от уравнения 10. Рассмотрим критическую скорость вращения ротора. Если приравнять пулю к определителю системы уравнений 6, то получим уравнение частоты. Лш — — В du — сГ 0, 11 Отсюда мы получаем 2 уравнения. D d а 4-s — 2 0 a c 1 — 4 0. 12 В этих уравнениях нет общих корней за исключением w 0, соответствующего отсутствию сил гироскопа. Вы можете легко проверить, добавив их. Из уравнения 12 определяется критическая угловая скорость.
Таким образом, ротор имеет 2 важные скорости вращения. Сравните эти критические значения скорости с собственной частотой вращения ротора задача 454. При вращении ротора число критических скоростей увеличивается в 2 раза, 1 из них делается меньше, а 2-я-больше собственной частоты вращения ротора. Если молекула радикала экспрессия критической скорости положительна s — 0 15 Для b a существует 2 важных скорости. В случае b a 1 значение критической скорости является действительным, а 2 — е значение-мнимым. Как видно из Формулы 7, при вынужденной вибрации Ротора, вызванной дисбалансом, возникает резонансная вибрация, соответствующая только 1 критической скорости. Этот.
При составлении дифференциальных уравнений движения надо рассматривать материальную точку в текущем Положении. Людмила Фирмаль
Скорость соответствует исчезновению правого знаменателя в 7 Б-д — с — 2 0. 16 Это критическое значение скорости совпадает с o1 13. Резонансная вибрация, соответствующая 2-му значению критической скорости Перемещение суммы 14 при условии текущей проблемы это не может произойти. Проблема 457. В условиях задачи 454 возмущающая сила Е действует на ротор, направлена параллельно оси y и определяет вынужденную вибрацию ротора при добавлении на расстоянии Неподвижная точка o. Проекция возмущающей силы на ось y изменяется в соответствии с формулой. Е е потому что я Где r0-максимальная возмущающая сила, а o-угловая скорость вращения самого Ротора.
Решение создайте разницу Специальные уравнения движения ротора с использованием теоремы об изменении основного момента ЛСУ-1— 3 У1 4 — е а, потому что ж. Если ввести значения 3 и 7 в уравнение 2, то оно будет выглядеть так b2, — to g 4- s 1-34 o 4-ДСЛ 4 — ы 2-04 5 1 — иди А1, потому что о. Конкретное решение уравнения 3, определяющее вынужденные колебания ротора, можно найти в следующем виде Г Б1 данные, 2 1П о. 4 4 подставляется в уравнение 3, cos 1 и 51p o Да 4- с —Ви с11 О кг-04-Б О 4-Добавить, — Гоа. Из уравнения 5, 1Ся значение ц и ц 5 Когда эти равные знаменатели станут геями, резонанс придет И ноль Д-в- СР—В0 1 0 С Отсюда вы получаете 2 важных значения скорости.
Так, в отличие от рассмотренных в предыдущих задачах вынужденных колебаний, вызванных дисбалансом Ротора, в данном случае резонанс возникает в 2 Значение скорости вращения ротора i. Найти отношение амплитуды вблизи резонанса, соответствующее 2-му значению критической скорости. Из 6 Л c1 b, nПН -. , 9 1, — назначение —. Sg-01. 1 Из уравнения 9 следует, что эти колебания приводят к тому, что ось ротора рисует конус в направлении, противоположном правильному вращению шпинделя.
Это движение называется обратным. Прецессирующий Ротор. Затем находим отношение амплитуды вблизи резонанса, соответствующее начальному значению критической скорости. У нас есть g г 1 n С1 1 — Н-Л. А, -а КСУ-o1l 1 л В этом случае движение оси ротора соответствует непосредственно precession. So, если вынужденное колебание вызвано определенной силой в направлении, то его величина изменяется с частотой При собственном вращении ротора возможны 2 типа колебаний, соответствующие обоим критическим значениям скорости 8.
Смотрите также:
Предмет теоретическая механика

