Оглавление:



Вынужденные колебания системы с одной степенью свободы. Резонанс
- Принудительная вибрация системы с определенной степенью свободы. Резонансной вынужденной вибрацией системы называют ее вибрацию, которая характеризуется внешней силой заклинивания F(0. Беспокойная сила может быть периодической и непериодической. Наибольшее практическое значение для расчета строительных конструкций имеет гармоническая нагрузка, которая изменяется по
закону синусоид или косинусов: F(O = f o s i n0/’ Где Fo-амплитудное значение нагрузки, 0-круговая частота мешающей нагрузки и/ — время. Рассмотрим систему с некоторой степенью свободы применительно к системе с гармоническим фокусом помех/7 (f)=F0sin0/(рис. 25.6). В этом случае уравнение динамического равновесия будет содержать силу F (0, и она примет форму),
в дополнение к восстанавливающей силе Fr и инерционной силе 5In: Людмила Фирмаль
2Y= — F+F — =0 Май * 71(О Огонь! t(d2y/d t2)+y / 6n=Fq sin0/. Разделить все члены уравнения на t, CO2=1 / / IBC: d2y / dt2+CO2y = Fo / y sin 0/, (25.6) Получено безразмерное обыкновенное дифференциальное уравнение второго порядка с постоянным коэффициентом. Полное решение этого уравнения состоит из общего решения соответствующего однородного уравнения (25.2) и частного решения неоднородного уравнения вида: cos co / B2sin co / — / — FQ6P / (1-02/CO2)sin0/. (25.7)
Первые два условия этого решения выражают свободное варьирование, а третье-принуждение. Сила резистора быстро ослабляет свободную вибрацию- 286gde Ust=Fo611-статическое смещение массы от амплитудного значения сжимающей нагрузки; CD=1/(1-02 / CO2) — амплитуда вынужденной вибрации больше статического смещения, вызванного максимальным значением сжимающей нагрузки. Устанавливается вынужденное колебание с частотой 0, тогда уравнение принимает вид: Y{1)^F0 6n/(l-0S /
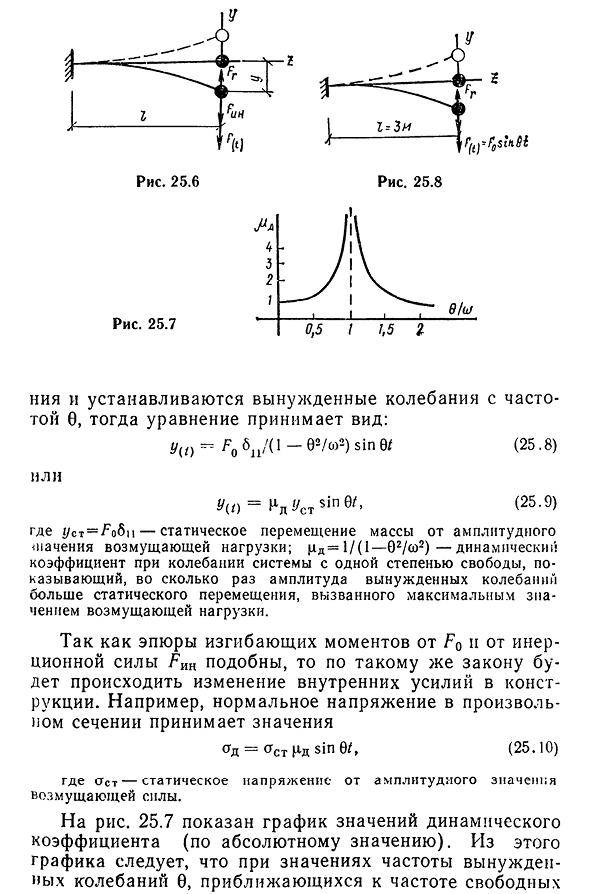
- U>S)синус / (25.8) Или Y(1)=Hn< / C Tsine/, (25.9) Поскольку диаграммы изгибающих моментов от сил инерции FQ и Lin аналогичны, то по одному и тому же закону происходит изменение внутренних сил в конструкции. Например, нормальное напряжение любого участка принимает значение Od=OST Nd sin0/, (25.10), где OST-статическое напряжение от амплитудного значения силы заклинивания. Для риса. 25.7 показан график значений динамических коэффициентов (по абсолютному значению). Из этого графика видно, что значение частоты вынужденной вибрации равно 0, приближаясь к частоте
свободы 287 вибрация co, динамический коэффициент увеличивается бесконечно. При совпадении частот (0=(o), возникает явление резонанса, и CD уходит в бесконечность. Фактически, при резонансе не происходит неконтролируемого увеличения амплитуды колебаний из-за наличия неупругого сопротивления. При проектировании строительных конструкций значения Со и 6 больше друг друга, последнее достигается либо изменением жесткости самой системы,либо применением специального оборудования-виброгасителей. Например. Определите динамический коэффициент и максимальное нормальное напряжение консольной стальной балки (рис. 25.8) от массы двигателя 0=20kN, f (t)=FuSin0/,
F0=5kN, числа оборотов n=240rpm, E==2,1-105MPa, F x=472cm3 и/x = 7080cm4. Людмила Фирмаль
Решение. Для консолей крайнего сечения 6P=P/3E JX=33/3-2,1-Yu5-10b смещение-7080-10-8= 0,605-10-«. Круговая свободная частота колебаний<o=K g/G8n=V9,81/20-103 -0,605-10—6 = 28,47 С Е-1. Круговая частота вынужденных колебаний 0=P2L / 60=240-2-3, 14/60=25,1 секунды-1. Динамический коэффициент И d =1/(1-eV©2) = 1 — (1 — 2 5 ,12/28,472) = 2,32. Максимальный изгибающий момент возникает при жесткой опоре балки от веса двигателя и динамической силы Fo: Mm ax=(G+rd Fo) Z= (20 + 5 • 2,32) 3 = (60 + 34,8) кн. Самое высокое нормальное давление опасного поперечного сечения луча dtah= = (60 + 34,8) 10-3/472-10~» = 127,1 + 73,7 = =200,8 МПа.
Смотрите также:
Решение задач по технической механике
| Понятие о колебаниях сооружений | Приближенный способ расчета на удар |
| Свободные колебания системы с одной степенью свободы | Основные понятия и расчетные схемы сооружений |

