Оглавление:






Вынужденные колебания системы с одной и двумя степенями свободы под действием синусоидальных возмущающих сил
- Когда возмущающие силы воздействуют на систему в течение всего процесса вибрации, возникают сложные колебания. Это результат суперпозиции вынужденных и свободных колебаний Система. Дифференциальные уравнения движения системы могут быть составлены с использованием уравнения Лагранжа. Из ДТ а л 57Ы- 3 0 Где 7-обобщенная координата системы, t-кинетическая энергия системы, ii-потенциальная энергия, а 0 — сила возмущения. Если система имеет 1 степень свободы, если 1 1 2, 1 1, 2. Для 2 степеней свободы, если подставить t и p в уравнение 1, получится система дифференциальных уравнений.
Здесь сила возмущения 2 0 считается изменяющейся в соответствии с законом синусоидальных волн в часто встречающихся случаях из-за относительной простоты математики это ограничивает ее рассмотрение Расчет и практическая значимость одновременно важны 3, 0 хорошо 81n 8, 0 h, 8 П П1 8. 3 Общее решение системы дифференциальных уравнений 2 состоит из общего решения однородной системы уравнений и частного решения неоднородной системы. Общее решение однородного Система представляет собой ранее рассмотренную свободную вибрацию и обнаруживается в соответствии с методом, указанным в 2 и 3 настоящей главы.
Для того, чтобы искусственный спутник, движущийся по орбите, концентричной с экватором, казался с Земли неподвижным, он должен быть расположенным на оси п, проходящей через спутник М, центр Земли О, а также через наблюдателя А, расположенного на экваторе и вращающегося вместе с Землей. Людмила Фирмаль
Поэтому мы сосредоточимся на определении конкретного решения для этого Система, которая представляет собой принудительную вибрацию системы. Я ищу частное решение в следующем формате. Tsu 51n p1, 7 01 81n p1. 4 Вводя эти значения в уравнение 2, мы попадаем в систему алгебраических уравнений. Н. -р н Бон-Р a1z ч, — р а ОГ Р Си-п а хорошо Где определяется неизвестный op o Детерминант этой системы исчезает rn-an —an — —an резонанс в случае 1 0, d f или a4.
В этом случае конкретное решение системы не найдено в виде 4. Дифференциальные уравнения движения системы также могут быть построены с использованием теоремы общей динамики. Для решения задачи определения вынужденной вибрации рекомендуется следующая последовательность действий Первый метод заключается в использовании уравнения Лагранжа. 1 Выбрать обобщенные координаты и настроить выражение кинетической энергии системы. 2 найти представление потенциальной энергии или вычислить обобщенную силу. 3 составить дифференциальное уравнение движения системы и ввести значение кинетической энергии и потенциальной энергии или обобщенной силы в уравнение Лагранжа.
Ищем конкретное решение дифференциального уравнения движения системы, находим амплитуду обобщенных координат. 5 приравнивая пулю к знаменателю представления амплитуды, мы можем видеть частоту возмущающей силы, в которой возникает резонанс. 2-й метод-это применение общей теоремы динамики. После выбора обобщенных координат системы дифференциальные уравнения движения непосредственно компилируются на основе выбранной теоремы динамики. Дальнейший ход решения такой же, как и в первом способе. Задача 451. Квадрату массы МХ находится на горизонтальной и абсолютно ровной плоскости.
Внутри коробки цилиндрических отверстий радиуса r находится шар b рисунок e с массой l2, размеры которого пренебрежимо малы. Коробка соединена с вертикальной стенкой пружиной, коэффициент жесткости которой равен s. Игнорируя трение между внутренней поверхностью шарика и коробкой, определяют вынужденную вибрацию системы, возникающую под действием периодической горизонтальной силы resepie. Выберите ось x, начиная с положения равновесия центра o коробки, и угол отклонения радиуса ob1 от вертикали будет 3. Радиус Вывода Обозначим через n давление шарика на коробку, направленное на запись дифференциального уравнения движения коробки.
- Создайте дифференциальное уравнение для абсолютного движения шара в проекции, перпендикулярной o k и ov. Абсолютное движение шара состоит из переносного поступательного движения и относительного вращения, центрированного на коробке и центре О. Поскольку переносное движение является поступательным движением, кориолисово ускорение шара равно нулю. Дифференциальное уравнение для движения шара в проекции перпендикулярной Оби выглядит следующим образом Р5-Р. В cos г -tzsh е 2 Вид дифференциального уравнения движения в проективном равен r 2- 5 н В-м д что Это 3 Решите 3 уравнения вместе, чтобы исключить-v. Л тг 31 н 4-sl — t. ГЬ 1п −7 потому что Го ш, я ГЗ х соз 81l — 0.
Эта система нелинейных дифференциальных уравнений не может быть интегрирована в замкнутом виде. Приблизительно 8 55, c08 p 1 можно поставить, ограничив его малыми колебаниями, игнорируя малые величины выше первичной десятичной дроби и представляя Формулы 4 и 5 в следующем виде l1x — — cx — go 51 n 01 О. 7 обозначим краткость- a2 −3 x a, где t1 pc 1p1 Х4-к Х-Л К 51 н 8 Г 0. 9 Принудительная вибрация определяется конкретным решением данной системы. Ищем конкретное решение в следующем формате Х Н1 кв. Р4 ПюЛ 10 Если вы введете эти значения в 8 и 9, то после простого преобразования вы увидите следующее О А2-о — xa a, o 0 2 — — i, got2 — 0, 11 Откуда А — р — к — 1С-Р 2 — Л О.
На какую высоту надо запустить искусственный спутник Земли для того, чтобы с Земли он казался неподвижным для наблюдателя, вращающегося пместе с Землей? Людмила Фирмаль
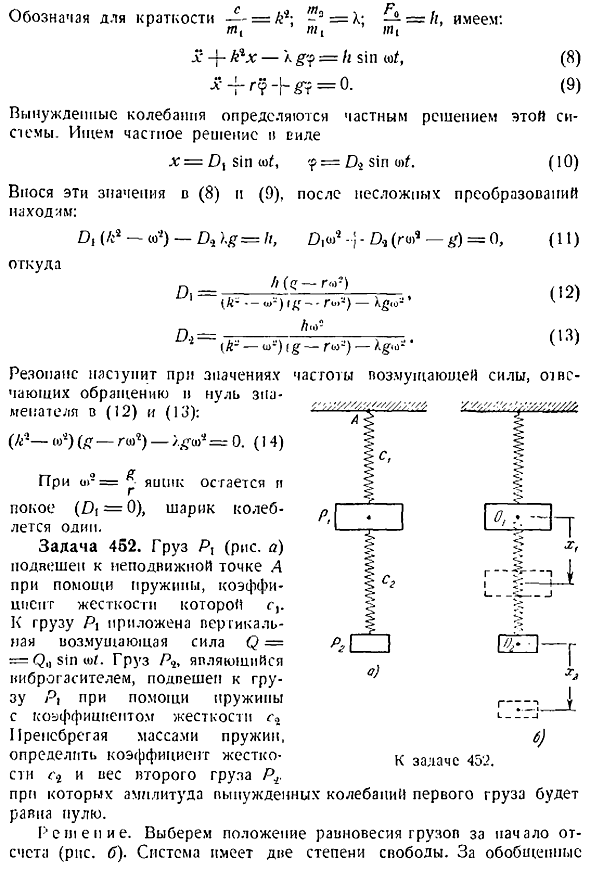
Резонанс возникает со значением, которое показывает знаменатели 12 и 13 в нуле. А2-а 0. 14 К—О 1 -г — это. — От частоты возмущающей силы, Если коробка остается неподвижной i, 0, шар будет вибрировать в одиночку. Задача 452. Нагрузка px рисунок a подвешивается к неподвижной точке a с помощью пружины, коэффициент жесткости которой равен c. Вертикальная сила взаимодействия 1181psh приложенная к нагрузке p. Нагрузка pb, колебательный демпфер, подвешивается к нагрузке p1 с помощью пружины с коэффициентом жесткости, игнорируя массу пружины для определения коэффициента жесткости и веса 2-й нагрузки p.
Амплитуда вынужденной вибрации первой нагрузки будет равна пуле. Решение. Выберите положение равновесия товара в начале координат рисунок b. Система имеет 2 степени свободы. Обобщенный 7. 7 м В координатах возьмем отклонение первой нагрузки от положения равновесия x и смещение второй нагрузки от положения равновесия x2. Затем к первой нагрузке прилагаются 3 силы сила упругости пружины в верхней части 1 — О Сила пружины p2 9 4 2 Сжимать силу Ф f051psh. 3 1-я сила приложена к 2-ой нагрузке. Сила упругости нижней пружины. Р3 — с, х, — х.
Создайте дифференциальное уравнение для движения товаров -с1×1 с9 х, -х, Оо31пш 5 6 Конкретное решение этой системы, определяющей вынужденные колебания груза, определяется в следующем виде, Х8 8 О0, x3 1n 0. 7 Присваивая значение переменной 7 выражениям 5 и 6, получаем c1 c2 — — c, o1 с- ш о, 0. Я Эти уравнения определяют амплитуду вынужденного колебания В соответствии с формулой 9 выбираются коэффициент жесткости 2-й пружины и масса ra, исключается амплитуда вынужденных колебаний 1-й нагрузки. С- Е И Поэтому при заданной частоте возмущающего усилия w всегда можно выбрать коэффициент жесткости дополнительной пружины и массу 2-го груза для поглощения вынужденного колебания 1-го load.
В этом случае необходимо обратить внимание на резонанс, который резонирует, когда знаменатели 9 и 10 исчезают. Е 3 — 0. 12 Величина угловой скорости, определяемая из уравнения 11, не удовлетворяет 9 и 10, так как не превращает знаменатель в пулю 12. Однако не всегда удается сохранить точно такое же значение.
Смотрите также:
Предмет теоретическая механика

