Оглавление:










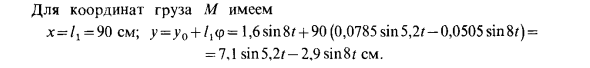

Вынужденные колебания системы без учета сопротивления
- Возбуждение вынужденных колебаний требует определенной формы воздействия на точку возмущенной механической системы. Наиболее распространенный случай силового и кинематического возбуждения. В этих случаях рассматриваются примеры линейных колебаний груза массой m вдоль горизонтальной плоскости (рис. 118, а) под действием пружины с жесткостью с. В зависимости от времени на нагрузку действует сила (Ф). Груз имеет одну степень свободы.
Галстук (гладкая поверхность) идеален. Созданы и обобщены уравнения Лагранжа для движения грузов. Рисунок 118 Координаты измеряются от положения нагрузки, где пружина не деформируется. У нас есть Сопротивление отсутствует, т. Е. (? F = 0. Кинетическая энергия нагрузки Потенциальная энергия и обобщенная сила 77 = cx2 / 2; Qn = -dP / dx = -cx. Для обобщенной силы QB, ‘8 г \ / (8х) = Ф8х / (8х) = Ф (г). Где 8 л — возможное движение груза в направлении увеличения х. Рассчитать производную кинетической энергии. У нас есть dT = .. £ dT dx mX ‘dt dx Подставляя полученное значение в уравнение Лагранжа, mx = -cxf-f (r) или dax + cx = f (f).
Так как механическая система, состоящая из точки переменной массы и отделившихся от нее частиц, свободна от действия внешних сил, то ее количество движения является постоянной величиной. Людмила Фирмаль
В случае гармонических помех QB = Φ (z) = H sin (p t +8). Где H, p и 8 — постоянные значения. Уравнение движения груза принимает вид mx + cx = Hsin (pf + 8). С той же проблемой перемещения груза, если сила Φ = 0 и, следовательно, QB = 0, но вместо этого перемещение конца пружинной точки A- в направлении оси Ox задано в виде z = z (t) Предположение (рис. 118, 6). Создайте лагранжево уравнение нагрузки для системы отсчета движения Ohu. Поскольку его начальная точка перемещается вместе с точкой A, OA всегда постоянна. В этом случае еще Q «= ~ dP) dx = -ex. Нагрузка кинетическая энергия 2 2.
Поскольку движение груза можно рассматривать как сложное, оно состоит из переносного переноса и точки A, которая связана с движущейся в данный момент системой координат Ohu. По теореме скорости абсолютная скорость движения v равна сумме соотношения рис движения и относительной скорости движения, то есть v = z + x. Производная кинетической энергии 1 £ 1- д <дх Подставляя полученное значение в уравнение Лагранжа, m (x + z) = -ex; mx + cx = -mz. Роль обобщенных сил в этом уравнении удовлетворяет значение -mz. Если точка A выполняет гармоническое колебание, z = zosin (p / 4-6), Где z0, p, 8 — постоянные значения.
В этом случае -mz = / nzop2sin (p / + 8) Дифференциальное уравнение для движения нагрузки принимает вид t x + cx = t zop2 sin (p t + 8). То есть так же, как в первом случае, но H = mzop2. Установка скорости точки A вместо z (t) изменится согласно гармоническому закону fx = z = zocine (pt + 8), Уравнение движения груза принимает вид mx + cx = mzopsin (pt + 8- ^ и в этом случае H = mzop. Основное различие в этих случаях состоит в том, что H не зависит от круговой частоты p при силовом возбуждении. При кинематическом возбуждении путем установки движения точки A z = zocine (pf + 8), пропорционального p2 и возбужденного путем установки скорости точки A z = zocine (pf + 8) , Пропорционально п.
Силовое возбуждение эквивалентно возбуждению путем установки точки ускорения. Дальнейшее рассмотрение вынужденных колебаний ограничивается силовым возбуждением. Обобщенная сила состоит из двух сил: потенциала Q «= -dP / da = -cq и гармонического возмущения QB = / 7sin (p / + 8). В зависимости от силы сопротивления обобщенная сила ξ) φ часть считается равной нулю. Константы H, p и 8, которые характеризуют гармоническую возмущающую силу, представляют собой амплитуду силы, круговую частоту и начальную фазу соответственно.
В этом случае из уравнения Лагранжа в предположении, что уравнения (2) и (3) справедливы для кинетической и потенциальной энергий, как в случае собственных линейных колебаний, дифференциальное уравнение aq + cq = Hsin ( получите pt + 8). (37) Разделим обе части (37) на a и введем обозначение k2 = c / a, h = H / a. Где k — круговая частота собственных колебаний, а h — относительная амплитуда возмущающей силы. Дифференциальное уравнение вынужденных колебаний без сопротивления в окончательном виде ^ + fc2 ^ = Асин (пр + 8). (38).
Получено неоднородное линейное дифференциальное уравнение второго порядка с постоянными коэффициентами. Согласно теории дифференциальных уравнений, решение состоит из общего решения равномерного уравнения qt и конкретного решения неоднородного уравнения q2. Общее решение уравнения (38) является суммой этих двух решений: = 4i + # 2 Однородное уравнение для определения qt, уравнение ql + k2qi = 0, согласуется с естественным колебательным дифференциальным уравнением. Поэтому решение qt называется естественной вибрацией системы. Это может быть выражено в двух эквивалентных форматах. ql = Clco & kt + C2sinkt = Al sin (Rg + oc). (39) Часть движения системы, характеризуемая функцией q2, является частным решением уравнения (38).
Эта часть движения называется вынужденной вибрацией системы. Функция q2 определяется по-разному в зависимости от соотношения частоты собственных колебаний и возмущающей силы. Рассматриваются два случая: отсутствие резонанса p / kn, резонанс при p = k. Пожалуйста, рассмотрите их. 1. Когда нет резонанса. Если резонанса нет, p = £ k, и конкретное решение q2 находится в том же виде, что и правая часть уравнения (38). = S sin (/ i + 8). (40) Константа B должна определяться из условия, что функция q2 является конкретным решением уравнения (38). Следовательно, если q2 назначено этому выражению, оно должно быть преобразовано в тождество.
Определите требуемую производную по времени от q2. = Bp cos (p / +3); q2 = -Bp2sin (pf + 8). Подставляя q2 и его производную в уравнение (38) и переводя все члены в одну часть, вы всегда получаете следующий действительный идентификатор. (-Bp2 + Bk2-A) sin (pt + 8) s0. Синус аргумента переменной не равен нулю для всех значений /, поэтому, если постоянный коэффициент в скобках синуса равен нулю, идентичность результата удовлетворяется: B (k2 — p2) –h = 0. Отсюда B = h / (k2-p2) Подстановка значения B в q дает вынужденную вибрацию формы ? 2 = p3psin (/ ’<+ 5). (41).
- Таким образом, движение системы характеризуется обобщенной координатой q. Состоит из двух колебаний разных частот — натурального qt с круговой частотой k и вынужденного q2 с круговой частотой p: q — qt + q2 = Ci cos kt + C2 sin Rm + p — p sin (pt + 8). (42) В амплитудном формате q = A, sinffcz-f-aJ + p-jSin ^ -l-S). (42 ‘) Константа С \ и С2 или и а! Определяется из начальных условий 1 = 0, q = q0, q = qo- Подставляя эти значения в уравнение (42) для q и q, где t = 0, +; 2-1 ‘jSinS; Rn = C2k + 1, л.с., cos8. To-R To-R Отсюда Ci = g0-, -2 * -2sinS; C2 = ^ — 2-cos8. К2-П2-К (К2-П2) Амплитуда собственных колебаний A] и начальная фаза a через Ct и C2 определяются как L, -7cG + c1tgα, -C, / C2. В результате амплитуда и начальная фаза собственных колебаний под воздействием возмущающей силы оказываются.
Не только из начального условия, но и из этого параметра силы, то есть естественная вибрация в этом случае может быть вызвана не только начальным условием, но и действием возмущения, даже когда начальное условие равно нулю. Введите амплитуду вынужденной вибрации 22 = / / (| k2-p21). Во-вторых, в зависимости от соотношения частот вынужденная вибрация может быть выражена в двух формах: Если p к k сдвиг фазы равен e = l. Фактически, сдвиг фазы как разность фаз между силой возмущения и вынужденной вибрацией e = (p <+8) — (pg + 8 — l) = rc. В этом случае вынужденная вибрация не в фазе с возмущающей силой. Это означает, что функция <72 (<) сведена к минимуму, особенно когда сила возмущения достигает максимума, и наоборот.
Но такие напряжения всегда имеются при невесомости вследствие естественной связи точек тела друг с другом, на которую можно влиять, например, термообработкой, изменением температуры и т. Людмила Фирмаль
Следовательно, вынужденная вибрация системы без сопротивления при p ^ k является гармонической вибрацией с постоянной амплитудой, возбуждаемой гармонизирующей силой возмущения. Их частота соответствует частоте возмущающей силы. Они полностью независимы от начальных условий. 2. В случае резонанса. Резонанс — это случай, когда частота собственных колебаний соответствует возмущающей силе, то есть p = k. Если частоты совпадают, вам нужно найти конкретное решение уравнения (38) в виде ^ 2 = / / cos (? (++ +8)). Константа B определяется из условия, что q2 является конкретным решением уравнения (38) и q2 становится тождеством. (38) заменить q2 и его производную и сделать постоянный коэффициент sin (/ ib 8) равным нулю [как в случае, когда члены Bt cos (pl + 8) исчезают друг от друга] B = -h / (2р).
Вынужденная вибрация выражается в виде «2 = — ^ s» (/ »+ S) = ^ ™ (^ P ‘+ S-NC) Основной особенностью вынужденных колебаний при резонансе является зависимость амплитуды от времени. На фиг. 119 Раунд матчей A2 = ht / (2р). В этом случае амплитуда вынужденной вибрации увеличивается пропорционально времени. Как видно из (43), фазовый сдвиг в резонансе равен π / 2. График вынужденной вибрации в резонансе, где круговая частота вынужденной вибрации на частоте среза возмущающей силы, q2, равна a = A2 = d // (2p) до q2 = -A2-ht / l2p. Поэтому (43) график вынужденных колебаний представляет собой синусоидальную волну, окруженную двумя прямыми ^ Y ‘= π / (2p) и q £’ = -ht / (2p), точки q2 = 0 и t = 0 Проходит (Рисунок 119).
Когда система движется, всегда существует сопротивление движению, поэтому рассматриваемый случай вибрации при резонансе без сопротивления фактически не встречается. Увеличение амплитуды из-за теоретически установленного линейного закона фактически не наблюдается, но амплитуда резонанса намного выше, чем при отсутствии резонанса. Эта характеристика вынужденной вибрации во время резонанса приводит к тому, что случайно возникающие резонансы в машинах, установках и конструкциях (мосты, роторы турбин, полы зданий и т. Д.) Могут привести к разрушению. Для вынужденной вибрации постройте графики амплитуды и фазового сдвига в соответствии с круговой частотой возмущающей силы.
У нас есть Здесь введено обозначение A2Q = h / k2 (рисунок 120). Если p-> k, величина Л2-> оо, но если p = k, эта формула для амплитуды вынужденных колебаний неприменима. Имеет место другая формула: A2 = ht / (2p). Рисунок 120 тг ^ ——- е Рисунок 121 График зависимости r от p (рис. 121) состоит из двух отрезков горизонтальной линии и одной точки, если p k r = n. Пример I. Нагрузка гравитации P = 20 Н подвешена на пружине (рис. 1 22), статическое удлинение под воздействием нагрузки> .с, = 5 см. Нарушение 5 = 20 грех 14 / N влияет на нагрузку. В первый момент пружина выдвигается, и X0 = 6 см, а скорость r0 = 10 см / с передается нагрузке. Napura Определите движение груза.
Решения. Ориентируйте ось Ox вертикально за пределы положения начала координат x O. Предположим, что возмущающая сила 5 направлена на положительную сторону оси Ox в момент времени t. Необходимо добавить гравитацию P и упругость пружины F. Линейное дифференциальное уравнение 2, F ^ P-F + S; P — F = P — c (ke Моя частота Выбери статику и пух! P = cX „; k2 = cg / P ~ 196 Разделим обе части уравнения на t. x + 196x = 980sinl4 /. Частота возмущения p = 14 с совпадает с k-колебанием. Там может быть резонанс. Собственная вибрация сила xl = Clcosl4 / + C2sinl4 /. Резонанс ф /, вибрация при 980 / x2 = -— cosl4 / = -—— cosl4 / = -35 / cos 14g. 2р 2-14 Генеральные грузоперевозки Скорость движения «= X = -14C1sinl4 / + I4C2cos14 / -35cos 14 / + 35-14 / sin 14 /.
Подстановка начальных значений f = 0, x = x0 = X0 — X „= 1 см, x = b0 = 10 см / с для x и x дает следующее уравнение для определения постоянной: 10 = 14С2-35. Их решение: С = 1 см; С2 = 3,2 см. Уравнение движения груза принимает вид x — cos 141 + 3.2sin 14 / -35 / cos 14 / cm. Уравнение естественной вибрации в амплитудном формате. У нас есть: — Д-р 5ф Кинетическая энергия системы только с массой груза рассчитывается по формуле Поскольку движение нагрузки можно считать сложным, поступательное перемещение с точкой O со скоростью y0 = lpcospt и относительно угловой скорости φ вокруг горизонтальной оси Oz через точку O, перпендикулярную стержню и плоскости Oxy Поскольку угол φ и угловая скорость φ, состоящие из вращательного движения, считаются малыми, скорость вращения вокруг оси равна /, φ и направлена вертикально вверх. Согласно теореме сложения скорости, ==) ‘0 + / 1ph.
Чтобы определить обобщенную силу, пусть система знает возможное движение r = 1С1 + (у0- / 2ф) — его удлинение. бар Thread она В положении статического равновесия момент силы тяжести и момент упругости для точки O равны друг другу, то есть P1 / 1 = cX.s, / g. Рассчитайте количество, содержащееся в левой части уравнения Лагранжа. После подстанции d P, 1c. -X Получить уравнение Лагранжа Однако, если „= -Ip2 sinpt .., копать cljg введение Diffsrentia: установка системы не может быть скомпилирована Используйте уравнение гранж. Применить относительные уравнения Вращающаяся дверь с учетом момента (стержень с грузом) Инерционная сила от конкретного движения. Введение в обозначения П, 1] 80-902 45 + 0,71) 1, Получите дифференциальное уравнение для следующей небольшой вибрации. 9 + A: 2
Решение φ = φ1 + φ2. здесь <₽! = C, COSKT + C2 думаю Общее решение естественных уравнений (естественная вибрация). Конкретное решение неравномерного уравнения (вынужденная вибрация), например, p * k. Вот так. <₽ = <?! coskt + C2 sin kt + p ———— sin / rt; φ = —Clksinkt + C2kcoskt + J1 ^, cospt. к-г Начальное условие задачи: (= 0, <p = 0, φ = 0. Подставляя значения этих уравнений в <p и φ, ; = 0,0785. № „н ч 8-1,86 C = 0; C2 = ——— = = ——— 1 2 к K2 — P2 5.2-36.8 Тогда решение дифференциального уравнения принимает вид.
Смотрите также:
Задачи по теоретической механике

