Оглавление:


Вынужденные колебания линейной системы при сопротивлении, пропорциональном скорости
- Вынужденные колебания линейных систем с сопротивлением, пропорциональным скорости. Если колебания линейных систем вызваны силами, действующими по некоторому закону, их называют
принудительными. Рассмотрен особый случай действия гармонических возмущающих сил: P = H sin 0 /, (10.47) где H — постоянная амплитуда силы. 0 — частота возмущающей силы.
т. Текущее время. Форма дифференциального уравнения для Людмила Фирмаль
вынужденных колебаний: y ‘+ 2nu’ + to2y = —— sin 0t, (10.48) и его интеграл с низким сопротивлением (n H _ м Y (до 2-0?) + 402n2 -1 / nR, (10.50) где уа — смещение системы от статического приложения максимального возмущения Рmax = //; коэффициент увеличения P-вибрации: 1 0 = 0 2 В 4p20 2 (10,51) График зависимости нуля от
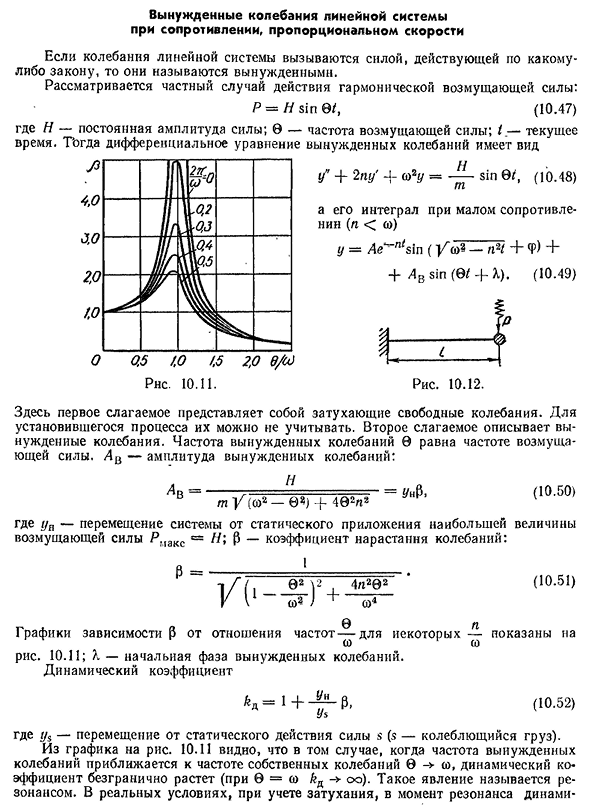
отношения частот показан в некоторых случаях на рисунке. 10,11; /. Начальная стадия вынужденной вибрации. Динамический коэффициент ^ d = 1 + 4! 1-P- (10,52) т / с, где ys — смещение силы s от статического воздействия (s — вибрационная нагрузка). Из графика
- видно, что динамический коэффициент увеличивается бесконечно, когда частота вынужденной вибрации 10.11 приближается к собственной частоте 0 (от 0 = до kRо®). Это явление называется резонансом. В реальных условиях следует учитывать динамику с учетом мгновенного затухания резонанса. 8 2-256 Коэффициент 225 не равен бесконечности, но достигает очень больших значений. Поэтому резонанс очень опасен для конструкции и не допускается. Чтобы
избежать резонанса, масса упругой системы, от которой зависит частота возмущения 0 и собственная частота со, изменяется. Если масса упругой системы важна по сравнению с массой вибрационной нагрузки s, собственная частота вибрации с учетом массы упругой системы составляет приблизительно (10.31a) Где у — деформация, вызванная статическим приложением нагрузки s + kQ, а Q — масса системы. k — принятый коэффициент уменьшения.
Для натяжения k = -i f согните простую балку k =. Пример. Определите максимальное Людмила Фирмаль
напряжение стальной балки I сечения № 16 (Jz = 873 см4, Wz = 109 см3), как показано на рисунке. 10,12. Размах луча I = 3 м. На нагрузку s = 3 кН (300 кгс), приложенную к концу, действует сила возмущения P = H sin Qt, H = 1 кН (100 кгс) и 0 = 15—. Масса балки Q игнорируется. Решения. Определите частоту собственных колебаний в соответствии с таблицей. 10.2 Найти массу вибрационной нагрузки: тогда 3000 9,81 = 306 м н с2 3EJ mL3 3 • 2 • 10e • 873 0,306 • 3003 = / 6 3 5 = 25,1 1 / с Динамический коэффициент, исключающий демпфирование колебаний, равен 1 /? d- 1 1 152 252 = 1,57. Изгибающий момент уплотнения L1d = 3000 • 3 + 1000 ■ -3 • 1,57 = 13,71 кН • м (137 100 кгс-см) и максимальное напряжение stmax- = = 137 108 = 126 МПа (1260 кгс / см2).
Смотрите также:
| Свободные незатухающие колебания | Расчеты на ударные нагрузки |
| Свободные затухающие колебания | Расчет по разрушающим нагрузкам |

