Оглавление:







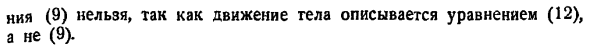

Вынужденные колебания без учета сил сопротивления
- Указывает обобщенную силу возмущения Q t. Тогда уравнение Лагранжа 2-го класса выглядит следующим образом. Где q-обобщенная координата системы, G-кинетическая энергия системы, а P-потенциальная энергия системы. Если предположить, что отклонение системы от положения устойчивого равновесия невелико, то кинетическую и потенциальную энергию можно представить в следующем виде G 1ad, 2 — Где A, C-положительные постоянные коэффициенты. a-коэффициент инерции, а c-квазикраффик coefficient. Вводя значение 1 в уравнение Лагранжа 2, получаем линейное неоднородное двумерное дифференциальное уравнение с постоянным коэффициентом. Нет. 3, 9 АА, 1 2 D. 4 Здесь, как и прежде, вводится обозначение c A k.
Решение дифференциальных уравнений 4, Если возмущающая сила Q t является синусоидальной функцией или может быть выражена в рядах Фурье, описано в Томе 2 Глава VIII, 4, п. 4.при произвольной зависимости от времени возмущающей силы решение уравнения 4 является уравнением м т 0 ОС КТ грех т в — J м р грех к т-р Ди 5 Где qa и — обобщенные координаты и обобщенные значения скорости системы в первый момент. Сумма первых 2-х элементов справа 5 определяет свободную вибрацию системы, которая возникает из-за сообщения, начального отклонения и начальной скорости к системе в равновесии. Я д0 потому что кцин КТ.
Так, если рассматривать систему, состоящую из двух соприкасающихся шаров, то давления первого шара на второй и второго шара на первый являются внутренними силами. Людмила Фирмаль
Раздел 2 справа от b определяет вынужденную вибрацию системы, возникающую под действием возмущенной силы Q t , приложенной к системе. Если эффект возмущения приложен к системе в виде единичного импульса 5 1, который прикладывается в первый момент к системе в стационарном состоянии, то последующее движение осуществляется по формуле П0 d81n 8 Эта функция называется откликом системы на один импульс. Если постоянная сила Q l приложена к покоящейся системе со временем t 0, то движение системы определяется следующим уравнением 4 t Л 1-008 0. 9 Эта функция, 0, называется реакцией системы на единичное возмущение или переходную проводимость.
Если вы хотите решить проблему принудительной вибрации систем с 1 степенью свободы, мы рекомендуем следующие шаги. 1 Выберите обобщенные координаты для определения местоположения системы. 2 выразить потенциальную и кинетическую энергию системы, выразить их в обобщенных координатах и обобщенной скорости. 3 выражение потенциальной и кинетической энергии вводится в уравнение Лагранжа типа 2 для получения дифференциального уравнения малых колебаний системы. 4 собственная частота сравнивается с частотой возмущающей силы, чтобы определить, есть ли резонанс. Б интегрируем дифференциальные уравнения колебаний и находим уравнение движения системы.
Задание 18.19. Вес PLT прямоугольные пластины, каждая из которых установлена на 4 симметричных жестких пружинах, имеют вес P двигателя. Двигатель имеет изогнутый шип с радиусом r, который вращается с постоянной угловой скоростью w. At на конце кривошипа, где масса игнорируется, крепится груз M веса Pr. Если предположить, что движение начинается из положения статического равновесия, а начальная скорость пластины равна нулю Уравнение движения пластины и собственная частота системы. Решение. Система имеет 1 степень свободы, положение которой определяется 1 обобщенной координатой x, вертикальным смещением от положения статического равновесия.
Такой вывод обусловлен тем, что угол поворота кривошипа является заданной функцией времени, а потому не может считаться 2-м углом. По вопросу 18.19. Обобщенные координаты, которые должны быть defined. To составьте уравнение Лагранжа 2-го рода, найдите потенциальную и кинетическую энергию системы. Обобщенная энергия положения системы записывается в виде P 0 4 e x Am 8 p1 k2 x r 1-owO const, Cj 4c-статический вариант 4 полных жестких пружин, пружины, которые могут быть определены из условий минимальной энергии положения в положении статического равновесия. Откуда ф л П. С.
Затем окончательное выражение потенциальной энергии системы Р- — п, п, п, л P8r L-cos wt 4-Константа 1 Кинетическая энергия системы состоит из 2 членов. 7 — Г1 Г Где 7 — кинетическая энергия двигателя, который движется в унисон с пластиной и пластиной, а Tt-кинетическая энергия груза, закрепленного на кривошипе. У нас есть 2 Найти кинетическую энергию нагрузки, предположив, что абсолютная скорость является геометрической суммой скорости полярного D и скорости вращательного движения относительно полярного D. Абсолютные значения переносной скорости и относительной скорости равны Ве я, ВР Р. Так… g, −4 1 Pi 5е 9 т здесь 90е — угол между вектором ve и vr. А. И.
- Лурье, аналитическая механика, Фнзматгиз, 1961, с. 195. Если мы суммируем 2 и 3, мы находим окончательное выражение кинетической энергии. T-g P, P. вы также можете использовать следующие команды 4 Перейдите к созданию уравнений Лагранжа типа 2. БН дл Ди Дим ДХ ДХ И-7 P1-P1. Р. −7 Р. й проекта р — — т ы С ы- Ф — , р — п п. ру 4. Вводя эти значения в 5, можно было бы Дж РЛ Ла4-П Х 4cx to2rcose. 6 Обозначая для краткости ФЭГ с п г ч ПиДжей П. П. РГ Р.
Запишите выражение 6 в следующем формате Х kgx-ч COS при, 7 Где A y p-собственная частота системы. Решением уравнения 7 является функция x x1×2.Где xx-общее решение соответствующего однородного уравнения X — — k x 0, а xx-частное решение уравнения 7. Итак… х cxcos в ЦС грех АФ с COS о. 8 Используйте начальные условия движения для определения любой интегральной константы. если T 0, х 0,х 0.Вводя эти значения переменных в 8 Получаем производную 8 X — кс Sin KT acacos KT-si N at.
Внешние силы могут переходить в разряд сил внутренних и, наоборот, внутренние силы могут переходить в разряд внешних при изменении состава системы. Людмила Фирмаль
Вводя в это уравнение 2-е начальное условие, находим c, 0.So, уравнение колебаний пластины выглядит следующим образом 0 Таким образом, движение пластины состоит из колебаний с частотами свободных колебаний участок 1 справа и вынужденных колебаний участок 2 справа. Задание 18.20.Масса M твердого тела движется по прямой горизонтальной гладкой направляющей под действием притяжения к центру O, пропорционального расстоянию от точки O. Центр инерции объекта приложена сила 1 коэффициент пропорциональности s .М Фе- Проводник вперед instructions.
В первый момент центр инерции совпал с центром О, и его скорость была равна нулю. Найдите вынужденное движение тела. Решение. Выберите ось x, которая соответствует горизонтальной направляющей, и сделайте центр O origin. To создайте дифференциальные уравнения движения, примените теорему к движению центра инерции проекции на ось X. У нас есть tx — съел Fe-al. 1 Где X-координата центра инерции тела. Запишите выражение 1 в следующем формате Х к х он — , 2 Где показано для краткости А Н. 3 Мы будем запускать дальнейшие решения в 2-х направлениях. 1 день пути.
Вместо заданной силы возмущения Q Fe-al мы применяем единичный мгновенный импульс S 1 к твердому телу во времени 0.Под действием этого импульса объект получает начальную скорость Однако начальное отклонение не получено. Таким образом, движение объекта при f 0 можно найти, интегрируя уравнение. 4-A x 0 Решением является реакция системы на один импульс 8×1 slnW. 4 Если единичный импульс приложен не в первый момент, а при t i, то вместо 4 движение тела описывается уравнением О в это страница по умолчанию для этого приложения.
Обозначим действие любой силы Q t на время от 0 до t как последовательное приложение минимального момента Ы г т — ДТ 6 согласно b , упражнение, вызванное основным упражнением dS, продукт 7 Результирующее движение определяется как суперпозиция движения, вызванного каждым фундаментальным импульсом. Таким образом, движение тела описывается определенным интегралом х-й вопрос а. СЛН ф-т,. с До сих пор любая сила возмущения Q 0 и результат 8 естественно согласуются с формулой 7.
Вводя значение Q f Fe al, получаем вывод. Это уравнение колебаний тела, когда начальное состояние движения равно нулю. 2-й способ. Решение линейного неоднородного дифференциального уравнения с постоянными коэффициентами Мы ищем решение всего Х к х его 2 Где Xi-общее решение однородного уравнения A A X 0 xj oscosа1 BsinA. 9 2-й член является частным решением полного уравнения 2.Ищите его в следующем формате ХВ Де-а. 10 после вычисления 2-й производной xt уравнение и г подставляется в уравнение 2. Д П Итак, Интеграл уравнения 2 равен х а со А B грех АФ М Л Е-ОИ. 12 Чтобы найти любые константы интегрирования A и B, используйте начальные условия x0 0 и A0 0 Для 0.
Когда вводятся первые начальные условия 13 Чтобы определить 2-ю произвольную константу, мы дифференцируем 12 относительно времени. Л — ла-грех КТ БК, потому что КТ-это я-и 14 14 если подставить 2-е начальное условие Откуда 15 Введение значения любой константы в решение 12 в конечном итоге приведет Tgetch pi — и 16 Это будет совпадать с решением, полученным первым методом. Обратите внимание, что вы можете определить любую интегральную константу из уравнения 9 невозможно.
Смотрите также:
Предмет теоретическая механика

