Выражение смешанного произведения через координаты
Пусть заданы векторы 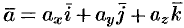 ,
, 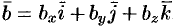 ,
, 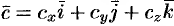 . Найдем их смешанное произведение, используя выражения в координатах для век торного и скалярного произведений:
. Найдем их смешанное произведение, используя выражения в координатах для век торного и скалярного произведений:
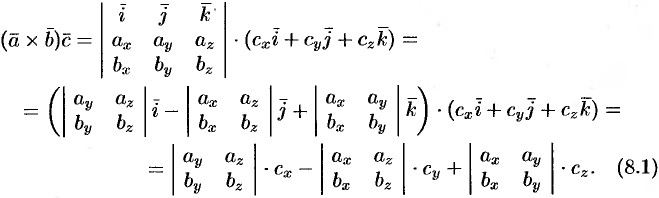
Полученную формулу можно записать короче:
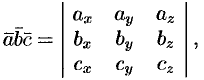
так как правая часть равенства (8.1) представляет собой разложение определителя третьего порядка по элементам третьей строки.
Итак, смешанное произведение векторов равно определителю третьего порядка, составленному из координат перемножаемых векторов.
На этой странице размещён полный курс лекций с примерами решения по всем разделам высшей математики:
Другие темы по высшей математике возможно вам они будут полезны:
| Выражение векторного произведения через координаты |
| Некоторые приложения векторного произведения |
| Некоторые приложения смешанного произведения |
| Параллельный перенос осей координат |

