Оглавление:
Выражение скалярного произведения через координаты
Пусть заданы два вектора
и 
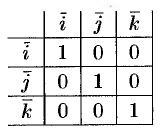
Найдем скалярное произведение векторов, перемножая их как многочлены (что законно в силу свойств линейности скалярного произведения) и пользуясь таблицей скалярного произведения векторов 
:
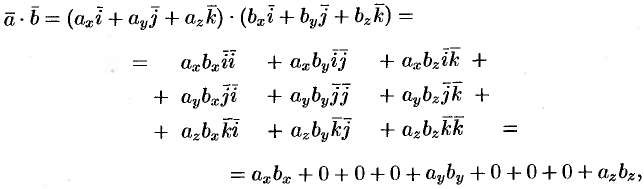
т.е.
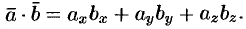
Итак, скалярное произведение векторов равно сумме произведений их одноименных координат.
Пример №6.2.
Доказать, что диагонали четырехугольника, заданного координатами вершин 
, взаимно перпендикулярны.
Решение:
Составим вектора 
и 
, лежащие на диагоналях данного четырехугольника. Имеем: 
и 
. Найдем скалярное произведение этих векторов:
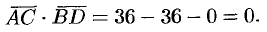
Отсюда следует, что 
. Диагонали четырехугольника 
взаимно перпендикулярны.
На этой странице размещён полный курс лекций с примерами решения по всем разделам высшей математики:
Другие темы по высшей математике возможно вам они будут полезны:
| Разложение вектора по ортам координатных осей |
| Скалярное произведение векторов и его свойства |
| Некоторые приложения скалярного произведения |
| Векторное произведение векторов и его свойства |
