Выражение количества движения системы через массу системы и скорость ее центра масс
При движении системы координаты ее точек 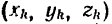 так же как и координаты центра масс системы
так же как и координаты центра масс системы 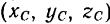 , изменяются.
, изменяются.
Из формулы (138) имеем:
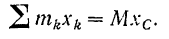
Взяв производные по времени от обеих частей данного равенства, получим:
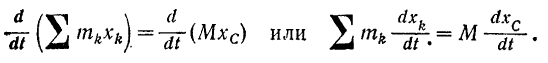
Но производная 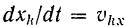 — проекции на ось
— проекции на ось 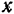 скорости
скорости 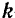 -й точки системы, а производная
-й точки системы, а производная 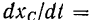
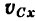 — проекции на ту же ось скорости центра масс системы.
— проекции на ту же ось скорости центра масс системы.
Следовательно,
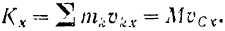
Проекция на какую-либо ось количества движения системы равна проекции на ту же ось количества движения центра масс системы, если положить, что в центра масс сосредоточена вся масса системы.
Проделывая аналогичные операции, будем иметь:
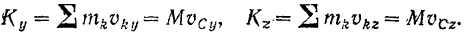
В левой части полученных равенств стоят проекции на соответствующие координатные оси количества движения системы
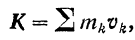
в правой части — проекции на те же оси количества движения центра масс 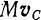 . Но если проекции двух векторов на три взаимно перпендикулярные оси равны между собой, то равны и сами векторы.
. Но если проекции двух векторов на три взаимно перпендикулярные оси равны между собой, то равны и сами векторы.
Следовательно,
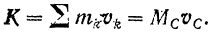
Количество движения любой системы равно количеству движения ее центра масс, если положить, что в центре масс сосредоточена вся масса системы.
Эта теория взята с полного курса лекций на странице решения задач с подробными примерами по предмету теоретическая механика:
Теоретическая механика — задачи с решением и примерами
Возможно вам будут полезны эти дополнительные темы:
| Об основных теоремах динамики |
| Количество движения точки и системы |
| Импульс силы |
| Теорема об изменении количества движения материальной точки с примерами решения |

